Exercice corrigé bac STI2D / STL - Métropole juin 2016 - Fonction logarithme
Logarithme et décibels
Exercice corrigé de mathématiques: Exercice corrigé du bac STI2D / STL - Métropole juin 2016 - Fonction logarithme: intensité acoustique et décibels
Exercice - énoncé:
Quand l'oreille humaine est soumise à une intensité acoustique,
exprimée en watts par mètre carré (W/m ), le niveau sonore du bruit
responsable de cette intensité acoustique est exprimé en
décibels (dB).
), le niveau sonore du bruit
responsable de cette intensité acoustique est exprimé en
décibels (dB).
Document
Cacher la correction
Document
Échelle de bruit
![$${|*{4}{c|}}\hline
\raisebox{.6cm}[1.8cm]{Sources sonores}
&\raisebox{.6cm}[1.8cm]{Intensit\'e acoustique (W/m$^2$)}
& \raisebox{.6cm}[1.8cm]{\begin{minipage}{2.5cm}Niveau sonore (dB) arrondi \'eventuellement \`a l'unit\'e\end{minipage}}
&\raisebox{.6cm}[1.8cm]{Sensation auditive}
\\\hline
D\'ecollage de la Fus\'ee Ariane&$10^ 6$ &180 &\multirow{3}{2.5cm}{Exige une protection sp\'eciale} \\\cline{1-3}
Turbor\'eacteur &$10^2$ &140 & \\\cline{1-3}
Course de Formule 1 &10 &130 & \\\hline
Avion au d\'ecollage &1 &120 &Seuil de douleur \\\hline
Concert et discoth\`eque &$10^{-1}$ &110
&\multirow{3}{3.4cm}{Tr\`es difficilement supportable}
\\\cline{1-3}
\raisebox{.4cm}[.3cm]{\begin{minipage}{4cm}Baladeur \`a puissance maximum\end{minipage}}
& \raisebox{.3cm}[1.1cm]{$10^{-2}$} &100 & \\\hline
Moto &$10^{-5}$ &70 &P\'enible \`a entendre \\\hline
Voiture au ralenti&$10^{-7}$ & 50 &Bruit courant\\ \hline
Seuil d'audibilit\'e &$10^{-12}$ &0,08 &Silence anormal \\\hline
$$](/Generateur-Devoirs/TSTI/Log/ex2016-Metropole/2.png)
![$${|*{4}{c|}}\hline
\raisebox{.6cm}[1.8cm]{Sources sonores}
&\raisebox{.6cm}[1.8cm]{Intensit\'e acoustique (W/m$^2$)}
& \raisebox{.6cm}[1.8cm]{\begin{minipage}{2.5cm}Niveau sonore (dB) arrondi \'eventuellement \`a l'unit\'e\end{minipage}}
&\raisebox{.6cm}[1.8cm]{Sensation auditive}
\\\hline
D\'ecollage de la Fus\'ee Ariane&$10^ 6$ &180 &\multirow{3}{2.5cm}{Exige une protection sp\'eciale} \\\cline{1-3}
Turbor\'eacteur &$10^2$ &140 & \\\cline{1-3}
Course de Formule 1 &10 &130 & \\\hline
Avion au d\'ecollage &1 &120 &Seuil de douleur \\\hline
Concert et discoth\`eque &$10^{-1}$ &110
&\multirow{3}{3.4cm}{Tr\`es difficilement supportable}
\\\cline{1-3}
\raisebox{.4cm}[.3cm]{\begin{minipage}{4cm}Baladeur \`a puissance maximum\end{minipage}}
& \raisebox{.3cm}[1.1cm]{$10^{-2}$} &100 & \\\hline
Moto &$10^{-5}$ &70 &P\'enible \`a entendre \\\hline
Voiture au ralenti&$10^{-7}$ & 50 &Bruit courant\\ \hline
Seuil d'audibilit\'e &$10^{-12}$ &0,08 &Silence anormal \\\hline
$$](/Generateur-Devoirs/TSTI/Log/ex2016-Metropole/2.png)
- D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, quelle semble être l'augmentation du niveau sonore ?
- La relation liant l'intensité acoustique
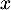 où
où 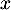 appartient à
l'intervalle
appartient à
l'intervalle 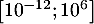 et le niveau sonore
est donnée par :
et le niveau sonore
est donnée par :
![\[f(x) =\dfrac{10}{\ln 10}\tm\ln(x) + 120.\]](/Generateur-Devoirs/TSTI/Log/ex2016-Metropole/6.png)
On pourra prendre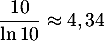 .
.
- Vérifier la conjecture émise à la question 1.
- Quel serait le niveau sonore de deux motos ?
- Pour éviter tout risque sur la santé, le port d'un casque de
protection acoustique est donc conseillé au delà de
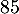 dB.
Déterminer l'intensité acoustique à partir de laquelle le port d'un
tel casque est conseillé.
dB.
Déterminer l'intensité acoustique à partir de laquelle le port d'un
tel casque est conseillé.
Correction exercice
- D'après le tableau, lorsque l'intensité acoustique est multipliée par 10, le niveau sonore semble augmenter de 10 dB.
-
- Si une intensité sonore
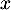 est multipliée par
est multipliée par 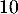 ,
alors le niveau sonore est
,
alors le niveau sonore est
![\[\begin{array}{ll}
f(10x)&=\dfrac{10}{\ln10}\ln(10x)+120\\[.8em]
&=\dfrac{10}{\ln10}\lp\ln(10)+\ln(x)\rp+120\\[.8em]
&=\underbrace{\dfrac{10}{\ln10}\ln(10)}+
\underbrace{\dfrac{10}{\ln10}\ln(x)+120}\\[.8em]
&=\qquad10\qquad+\qquad f(x)
\enar\]](/Generateur-Devoirs/TSTI/Log/ex2016-Metropole_c/3.png)
Ainsi, le niveau sonore est bien augmenté de 10. - L'intensité acoustique pour une moto est
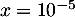 ,
donc pour deux motos de
,
donc pour deux motos de 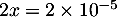 .
.
Le niveau sonore correspondant est alors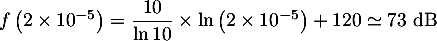
- Si une intensité sonore
- L'intensité acoustique à partir de laquelle un tel casque est
conseillé est telle que
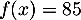 ,
soit
,
soit
![\[\begin{array}{ll}
\dfrac{10}{\ln 10}\tm\ln(x) + 120=85
&\iff \ln(x)=\dfrac{(85-120)\tm\ln10}{10}\\[.8em]
&\iff x=e^{-3,5\tm\ln10}\simeq 3\tm10^{-4}\text{ W/m}^2
\enar\]](/Generateur-Devoirs/TSTI/Log/ex2016-Metropole_c/8.png)
Cacher la correction
Voir aussi: