Exercice corrigé: Résolution d'équations pleines de fractions
Fractions et équation quotient nul
Seconde générale
Exercice corrigé de mathématiques: Exercice corrigé: Résolution d'équations pleines de fractions - Equation quotient nul
Exercice - énoncé:
Résoudre les équations:
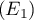 :
: 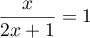
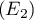 :
: 
 :
: 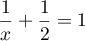
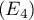 :
: 
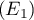 :
:
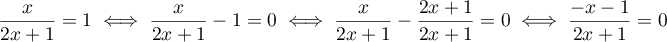
C'est une équation quotient, et donc,
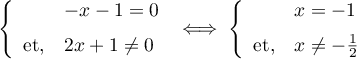 ,
d'où
,
d'où 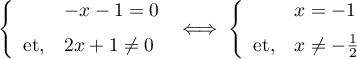 .
.
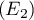 :
:
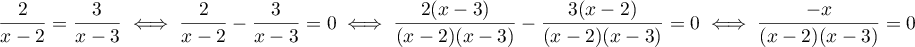 .
.
C'est une équation quotient, et donc,
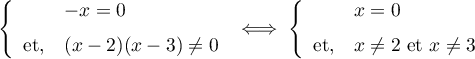 ,
d'où,
,
d'où,
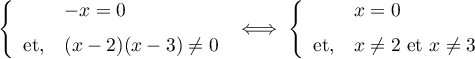 .
.
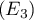 :
:
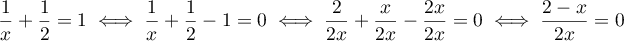 .
.
C'est une équation quotient et donc,
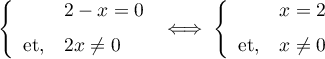 ,
d'où,
,
d'où,
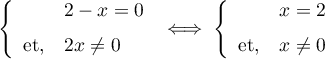 .
.
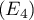 :
:
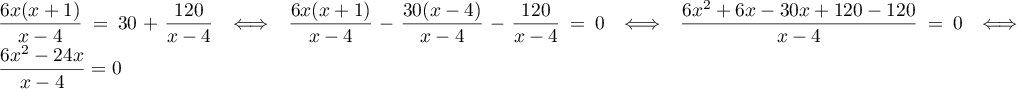
On peut, et doit, factoriser le numérateur: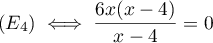
C'est une équation quotient, et donc,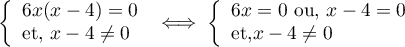
Finalement, cette équation a une seule solution: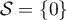 .
.
Cacher la correction
Correction exercice
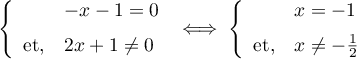 ,
d'où
,
d'où 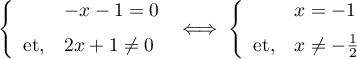 .
.
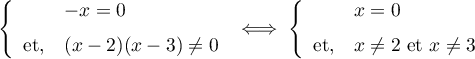 ,
d'où,
,
d'où,
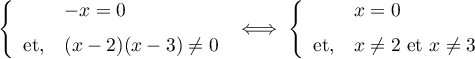 .
.
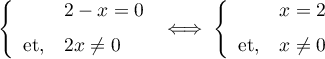 ,
d'où,
,
d'où,
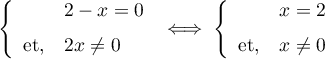 .
.
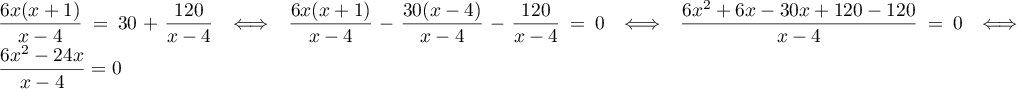
On peut, et doit, factoriser le numérateur:
C'est une équation quotient, et donc,
Finalement, cette équation a une seule solution:
Cacher la correction
Voir aussi: