Exercice corrigé - Etude d'une fonction avec paramètres
Etude à l'aide d'une fonction auxiliaire
Première générale et scientifique
Exercice corrigé de mathématiques: Exercice corrigé - Etudes de fonctions, à l'aide d'une fonction auxiliaire et du théorème des valeurs intermédiaires
Exercice - énoncé:
- On appelle
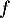 la fonction définie sur
la fonction définie sur 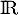 par l'expression
par l'expression
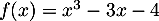 .
.
- Etudier les variations de
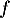 , et dresser son tableau de
variation.
, et dresser son tableau de
variation.
- Montrer que l'équation
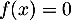 a une unique solution
a une unique solution 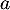 sur
sur 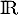 et que
et que ![$a\in[2;3]$](/Generateur-Devoirs/1S/Chap3/ex3/8.png) .
.
Donner un encadrement de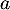 d'amplitude
d'amplitude 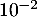 .
.
- Déterminer le signe de
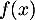 sur
sur 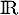 .
.
- Etudier les variations de
- On appelle
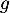 la fonction définie sur
la fonction définie sur 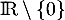 par
par
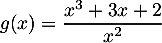 .
.
- Calculer la dérivée
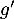 de
de 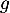 et montrer que
et montrer que
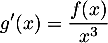 pour tout
pour tout 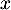 de
de 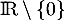 .
.
- En déduire les variations de
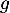 .
.
- Montrer que
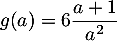 .
.
En déduire un encadrement de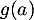 .
.
- Calculer la dérivée
Correction exercice
- On appelle
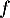 la fonction définie sur
la fonction définie sur 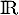 par l'expression
par l'expression
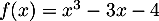 .
.
-
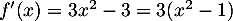 , et donc,
, et donc,
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-1$ && $1$ && $+\infty$ \\\hline
$f'(x)$ && $+$ & \zb& $-$ &\zb&$+$ & \\\hline
&&&-2&&&&\\
$f(x)$ &&\psline{->}(-0.4,-0.3)(0.5,0.6)&&
\psline{->}(-0.4,0.6)(0.5,-0.3)&&
\psline{->}(-0.4,-0.3)(0.6,0.6)&\\
&&&&&-6&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/ex3_c/5.png)
- La fonction
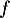 est dérivable sur
est dérivable sur ![$[2;3]$](/Generateur-Devoirs/1S/Chap3/ex3_c/7.png) ,
strictement croissante, et telle que
,
strictement croissante, et telle que 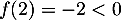 et
et 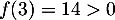 .
.
On en déduit, d'après le théorème de la bijection, que l'équation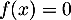 admet une unique solution sur
admet une unique solution sur ![$[2;3]$](/Generateur-Devoirs/1S/Chap3/ex3_c/11.png) .
.
De plus, sur![$]-\infty;2]$](/Generateur-Devoirs/1S/Chap3/ex3_c/12.png) , le maximum de
, le maximum de 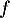 est
est 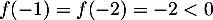 , et donc l'équation
, et donc l'équation 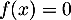 n'a pas de solution.
n'a pas de solution.
De même, sur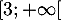 , la fonction est croissante et a pour minimum
, la fonction est croissante et a pour minimum 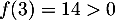 , et l'équation
, et l'équation 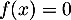 n'y admet pas non plus de solution.
n'y admet pas non plus de solution.
En résumé, l'équation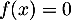 admet une unique solution sur
admet une unique solution sur 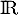 , et cette solution appartient à l'intervalle
, et cette solution appartient à l'intervalle ![$[2;3]$](/Generateur-Devoirs/1S/Chap3/ex3_c/21.png) .
.
De plus, on calcule que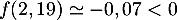 et
et
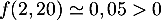 , d'où l'encadrement
, d'où l'encadrement
![\[2,19<a<2,20\]](/Generateur-Devoirs/1S/Chap3/ex3_c/24.png)
- On en déduit le signe de
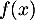 sur
sur 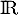 :
:
![\[\begin{tabular}{|c|ccccccccc|}\hline
$x$ & $-\infty$ && $-1$ && $1$ && $a$ && $+\infty$ \\\hline
&&&-2&&&&&&\\
$f(x)$ &&\psline{->}(-0.4,-0.3)(0.6,0.6)&&
\psline{->}(-0.4,0.6)(0.5,-0.3)&&
\psline{->}(-0.4,-0.3)(1.4,0.6)&\rput(0,0.12){$0$}&&\\
&&&&&-6&&&&\\\hline
$f(x)$ &&&$-$&&&&\zb& $+$&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/ex3_c/27.png)
-
- On appelle
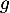 la fonction définie sur
la fonction définie sur 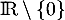 par
par
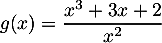 .
.
- On a
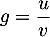 , avec
, avec
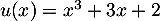 ,
, 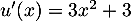 , et
, et
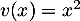 ,
, 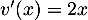 , d'où,
, d'où,
![\[\begin{array}{ll}g'(x)
&=\dfrac{(3x^2+3)x^2-(x^3+3x+2)(2x)}{x^4}\\
&=\dfrac{x^4-3x^2-4x}{x^4}\\
&=\dfrac{x^3-3x-4}{x^3}
=\dfrac{f(x)}{x^3}
\enar\]](/Generateur-Devoirs/1S/Chap3/ex3_c/36.png)
- On déduit de la question 1.c) le tableau de variation:
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $0$ && $a$ && $+\infty$ \\\hline
$f(x)$ && $-$ &$|$ & $-$ &\zb& $+$ & \\\hline
$x^3$ && $-$ &\zb&$+$ &$|$ & $+$ & \\\hline
$g'(x)$ && $+$ & \mbox{$\hspace{0.1em}|\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$} & $+$ & \\\hline
&&&\psline(0,-1.2)(0,0.3)\,\psline(0,-1.2)(0,0.3)&&&&\\
$g(x)$ &&\psline{->}(-0.4,-0.3)(0.6,0.6)&&
\psline{->}(-0.4,0.6)(0.5,-0.3)&&
\psline{->}(-0.4,-0.3)(0.6,0.6)&\\
&&&&&$g(a)$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/Chap3/ex3_c/37.png)
- On a, par définition du nombre
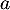 ,
, 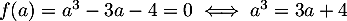
On en déduit que
![\[\begin{array}{ll}g(a)&=\dfrac{a^3+3a+2}{a^2}\\
&=\dfrac{(3a+4)+3a+2}{a^2}\\
&=\dfrac{6a+6}{a^2}\\
&=6\dfrac{a+1}{a^2}\enar\]](/Generateur-Devoirs/1S/Chap3/ex3_c/40.png)
On a vu de plus que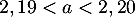 et alors,
et alors,
- d'une part
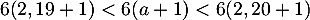
- et d'autre part
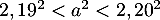 et alors
et alors
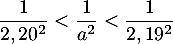
![\[\dfrac{6(2,19+1)}{2,20^2}<\dfrac{6(a+1)}{a^2}<\dfrac{6(2,20+1)}{2,19^2}\]](/Generateur-Devoirs/1S/Chap3/ex3_c/45.png)
et on trouve donc finalement l'encadrement
![\[3,95<g(a)<4,00\]](/Generateur-Devoirs/1S/Chap3/ex3_c/46.png)
- d'une part
- On a
Cacher la correction
Voir aussi: