Un trinôme d'élèves qui connaissent leur cours ?

Exercice corrigé - maths en seconde générale

Énoncé

Dans une classe de 30 élèves, 10 élèves connaissent parfaitement leur cours.
Je désigne dans cette classe successivement trois élèves au hasard pour former un groupe de travail.
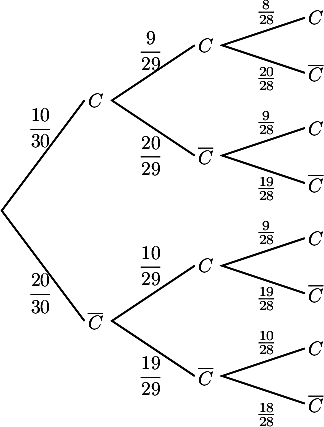
  1. Dresser un arbre de probabilités décrivant la situation.
  2. Quelle est la probabilité pour que, dans ce groupe, aucun élève ne connaisse parfaitement son cours ?
  3. Quelle est la probabilité pour que tous les élèves du groupe connaissent parfaitement leur cours ?
  4. Quelle est la probabilité pour qu'au moins un élève du groupe connaisse parfaitement son cours ?



Correction

Correction

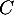1. On note $C$:"l'élève désigné connaît parfaitement son cours"


$$(-0.5,-3.4)(5,3.8) \psline(1.5,2)(0,0)(1.5,-2) \rput(0.7,1.5){$\dfrac{10}{30}$}\rput(1.7,2){$C$} \rput(0.7,-1.5){$\dfrac{20}{30}$}\rput(1.7,-2){$\overline{C}$} % \psline(3.5,3)(2,2)(3.5,1) \rput(2.7,2.9){$\dfrac{9}{29}$}\rput(3.7,3){$C$} \rput(2.7,1){$\dfrac{20}{29}$}\rput(3.7,1){$\overline{C}$} % \psline(5.5,3.5)(4,3)(5.5,2.5) \rput(4.8,3.6){$\frac{8}{28}$}\rput(5.7,3.5){$C$} \rput(4.8,2.4){$\frac{20}{28}$}\rput(5.7,2.5){$\overline{C}$} \psline(5.5,1.5)(4,1)(5.5,.5) \rput(4.8,1.6){$\frac{9}{28}$}\rput(5.7,1.5){$C$} \rput(4.8,.4){$\frac{19}{28}$}\rput(5.7,.5){$\overline{C}$} %% \psline(3.5,-3)(2,-2)(3.5,-1) \rput(2.7,-3){$\dfrac{19}{29}$}\rput(3.7,-3){$\overline{C}$} \rput(2.7,-1){$\dfrac{10}{29}$}\rput(3.7,-1){$C$} % \psline(5.5,-3.5)(4,-3)(5.5,-2.5) \rput(4.8,-3.7){$\frac{18}{28}$}\rput(5.7,-3.5){$\overline{C}$} \rput(4.8,-2.4){$\frac{10}{28}$}\rput(5.7,-2.5){$C$} \psline(5.5,-1.5)(4,-1)(5.5,-.5) \rput(4.8,-1.6){$\frac{19}{28}$}\rput(5.7,-1.5){$\overline{C}$} \rput(4.8,-.4){$\frac{9}{28}$}\rput(5.7,-.5){$C$} $$

2. $P=\dfrac{20}{30}\tm\dfrac{19}{29}\tm\dfrac{18}{28}=\dfrac{57}{203}\simeq 0,28$
 
3. $P=\dfrac{10}{30}\tm\dfrac{9}{29}\tm\dfrac{8}{28}=\dfrac{6}{203}\simeq 0,030$
 
4. L'événement "Au moins un élève connaît parfaitement son cours" est le contraire de "aucun élève ne connaît son cours".
Ainsi, d'après la question 2., la probabilité est d'environ $1-\dfrac{57}{203}=\dfrac{146}{203}\simeq0,72$.


Tag:Probabilités

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs