Production de poutrelles parfois défectueuses
Exercice corrigé - maths en seconde générale
Énoncé
Une société fabrique des poutrelles métalliques dans deux usines 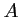 et
et 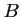 .
En une semaine, elle fabrique
.
En une semaine, elle fabrique 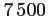 poutrelles, parmi lesquelles
certaines sont défectueuses.
poutrelles, parmi lesquelles
certaines sont défectueuses.
L'usine ![]() en a fabriqué
en a fabriqué ![]() , dont 1% sont
défectueuses et l'usine
, dont 1% sont
défectueuses et l'usine ![]() a fabriqué le reste, dont 6% sont
défectueuses.
a fabriqué le reste, dont 6% sont
défectueuses.
On prend au hasard une poutrelle dans la production de la semaine.
- Calculer la probabilité de l'événement
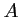 : "la poutrelle provient de l'usine
: "la poutrelle provient de l'usine 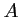 ",
ainsi que la probabilité de l'événement
",
ainsi que la probabilité de l'événement
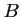 : "la poutrelle provient de l'usine
: "la poutrelle provient de l'usine 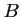 ".
".
- Combien de poutrelles produites par l'usine A pendant cette
semaine sont défectueuses ?
- Réaliser un arbre des probabilités décrivant complètement la
situation.
- Calculer la probabilité qu'une poutrelle prise au hasard soit défectueuse.
Correction
Correction
- Il y a 7500 poutrelles produites dont 3000 par l'usine A.
On a donc
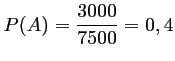 .
.
De même, il y a
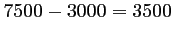 poutrelles produites dont 3000 par
l'usine B.
On a donc
poutrelles produites dont 3000 par
l'usine B.
On a donc
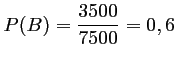 .
.
- Il y a
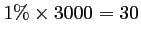 poutrelles défectueuses produites par
l'usine A cette semaine.
poutrelles défectueuses produites par
l'usine A cette semaine.
- On note
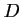 l'événement: "la poutrelle prélevée est
défectueuses".
l'événement: "la poutrelle prélevée est
défectueuses".
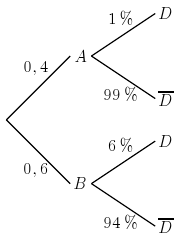
- En utilisant l'arbre précédant, on a alors:
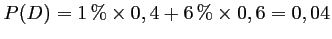 .
.
Tag:Probabilités
Voir aussi:
Quelques devoirs
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
probabilités (arbres de probabilités), et quelques inéquations (tableaux de signes)
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: patisserie à la crème ou aux fruits
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: véhicules avec d'éventuels problèmes de frein et/ou d'éclairage
tableau de signe - Équations cartésienne de droites - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: au hasard, une pièce truquée ou une équlibrée
