Probabilité de la réunion et de l'intersection (2)
Exercice corrigé - maths en seconde générale
Énoncé
Une campagne de prévention routière s'intéressant aux défauts constatés
sur le freinage et sur l'éclairage de 400 véhicules a révélé que:
60 des véhicules présentent un défaut de freinage,
140 présentent un défaut d'éclairage,
et 45 présentent à la fois un défaut de freinage et un
défaut d'éclairage.
- On choisit un véhicule au hasard parmi ceux qui ont été
examinés.
Donner la probabilité, sous forme de fraction irréductible, que:- le véhicule présente un défaut de freinage mais pas de défaut d'éclairage ?
- le véhicule présente un défaut d'éclairage mais pas de défaut de freinage ?
- le véhicule ne présente aucun des deux défauts ?
- le véhicule présente au moins un des deux défauts ?
- Je suis monté dans un de ces véhicules. Son éclairage ne fonctionne pas. Quelle est la probabilité qu'il ne freine pas correctement ?
Correction
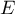 : "Le véhicule présente un défaut
d'éclairage" et
: "Le véhicule présente un défaut
d'éclairage" et 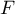 : "Le véhicule présente un défaut de freinage".
: "Le véhicule présente un défaut de freinage".
Correction
On note les événements:
Avec un diagramme: 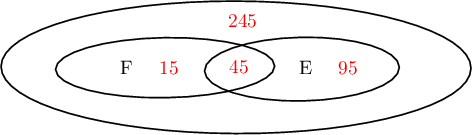 |
Avec un tableau: 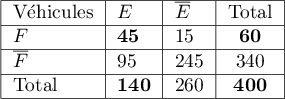 |
-
a)
 b)
b) 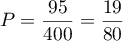 c)
c) 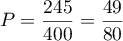 d)
d) 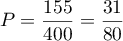
-
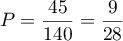
Tag:Probabilités
Voir aussi:
Quelques devoirs
pourcentage et probabilités, et deux tableaux de signes. Intersection de deux courbes
probabilités (arbres de probabilités), et quelques inéquations (tableaux de signes)
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: patisserie à la crème ou aux fruits
tableau de signe - Intersection et position relative de deux courbes - Taux d'évolution successifs - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: un jeu avec un dé - Probabilité: véhicules avec d'éventuels problèmes de frein et/ou d'éclairage
tableau de signe - Équations cartésienne de droites - Système d'équations - Équations cartésienne de droites et intersection de droites - Probabilité: au hasard, une pièce truquée ou une équlibrée
