Deux fonctions affines et des intersections
Exercice corrigé - maths en seconde générale
Énoncé
Soit 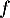 et
et 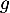 les fonctions
définies par les expressions
les fonctions
définies par les expressions
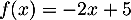 et
et
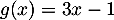 .
.
On note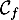 et
et 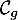 les courbes représentatives
de ces deux fonctions.
les courbes représentatives
de ces deux fonctions.
On note
- Déterminer les coordonnées du point
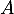 d'intersection
de
d'intersection
de 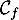 avec l'axe des ordonnées, et du point
avec l'axe des ordonnées, et du point
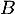 d'intersection de
d'intersection de 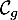 avec l'axe des abscisses.
avec l'axe des abscisses.
- Tracer
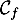 et
et 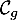 dans un repère.
dans un repère.
- Calculer les coordonnées du point d'intersection de
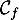 et
et 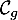 .
.
Correction
Correction
- Soit
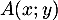 alors comme
alors comme 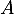 appartient à l'axe des ordonnées,
on a
appartient à l'axe des ordonnées,
on a 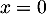 , et, comme
, et, comme 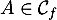 ,
, 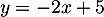 soit, avec
soit, avec 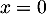 ,
,
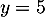 .
Ainsi on trouve
.
Ainsi on trouve 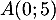 .
.
Soit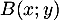 alors comme
alors comme 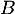 appartient à l'axe des abscisses,
on a
appartient à l'axe des abscisses,
on a 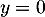 , puis comme
, puis comme 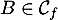 , on a
, on a 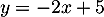 soit, avec
soit, avec 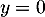 ,
,
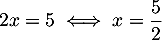 .
Ainsi, on trouve
.
Ainsi, on trouve 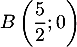 .
.
-
![\[\psset{unit=.7cm,arrowsize=7pt}
\begin{pspicture}(-1,-2)(4,5.5)
\psline{->}(-1.2,0)(4,0)
\psline{->}(0,-2)(0,6)
\multido{\i=-1+1}{7}{\psline(.1,\i)(-.1,\i)\rput(-.2,\i){\i}}
\multido{\i=-1+1}{5}{\psline(\i,.1)(\i,-.1)\rput(\i,-.3){\i}}
\psplot{-.5}{3}{-2 x mul 5 add}\rput(2.5,.8){$\mathcal{C}_f$}
\psplot{-.3}{2}{3 x mul 1 sub}\rput(2.3,4.6){$\mathcal{C}_g$}
\end{pspicture}\]](/Generateur-Devoirs/2nde/Chap4/exFAI_c/17.png)
- Soit
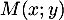 le point d'intersection de
le point d'intersection de 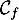 et
et  , alors on a
, alors on a
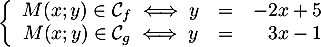
d'où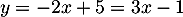 donc
donc
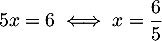 ,
et alors
,
et alors 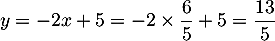 .
.
Ainsi, le point d'intersection est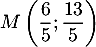 .
.
Tags:AllSystèmes
Voir aussi:
