Ligne en pointillés dans canvas
Style en javascript
… ou comment tracer des lignes en pointillés (line style: dashed)
On trace une ligne en pointillés en alternant de courts segments.
La fonction globale DashedLine(xA,yA,xB,yB,L,l) trace ceci, en utilisant 6 paramètres:
-
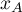 et
et 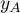 : les coordonnées du point
: les coordonnées du point 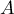 , une des deux extrémités du segment
, une des deux extrémités du segment ![$[AB]$](canvas-line-style-pointilles-dashed-IMG/4.png)
-
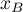 et
et 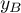 : les coordonnées du point
: les coordonnées du point 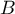 , l'autre extrémité du segment
, l'autre extrémité du segment ![$[AB]$](canvas-line-style-pointilles-dashed-IMG/8.png)
-
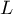 et
et 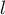 les deux longueurs, en pixels, respectivement de la
longueur des tirets utilisés et de l'espacement entre chque tiret.
les deux longueurs, en pixels, respectivement de la
longueur des tirets utilisés et de l'espacement entre chque tiret.
![\psset{unit=1.2cm}\begin{pspicture}(-.5,-.5)(8.2,1.8)
\newcommand{\f}[1]{#1 .7 add}
\multido{\i=0+1}{8}{\psline[linewidth=1.8pt](\i,1)(! \f{\i}\space1)}
\psline[linewidth=.3pt](2,1.2)(2,0)
\psline[linewidth=.3pt](2.7,1.2)(2.7,0)
\psline[arrowsize=6pt,linewidth=.3pt]{<->}(2.,.2)(2.7,.2)
\rput(2.35,-.1){$L$}
\psline[linewidth=.3pt](4.7,1.2)(4.7,0)
\psline[linewidth=.3pt](5,1.2)(5,0)
\psline[arrowsize=6pt,linewidth=.3pt]{->}(4.2,.2)(4.7,.2)
\psline[arrowsize=6pt,linewidth=.3pt]{<-}(5,.2)(5.5,.2)
\psline[linewidth=.3pt](4.7,.2)(5,.2)
\rput(4.85,-.1){$l$}
\rput(0,.98){$\bullet$}\rput(0,1.2){$A$}
\rput(7.7,.98){$\bullet$}\rput(7.7,1.2){$B$}
\end{pspicture}](canvas-line-style-pointilles-dashed-IMG/11.png)
Exemples de valeurs pour
![\psset{unit=1.2cm}\begin{pspicture}(-.3,-.3)(8.2,2.7)
\newcommand{\f}[1]{#1 .7 add}
\multido{\i=0+1}{8}{\psline[linewidth=1.5pt](\i,2)(! \f{\i}\space2)}
\rput[l](0,2.2){$L=0,7$, $l=0,3$}
\renewcommand{\f}[1]{#1 .9 add}
\multido{\i=0+1}{8}{\psline[linewidth=1.5pt](\i,1)(! \f{\i}\space1)}
\rput[l](0,1.2){$L=0,9$, $l=0,1$}
\renewcommand{\f}[1]{#1 .5 add}
\multido{\i=0+1}{8}{\psline[linewidth=1.5pt](\i,0)(! \f{\i}\space0)}
\rput[l](0,.2){$L=l=0,5$}
\end{pspicture}](canvas-line-style-pointilles-dashed-IMG/14.png)
Code javascript et exemples d'utilisation
- Code: Select all
-
<canvas id="canvas" width="300" height="200" style="border: 2px solid black;"></canvas>
<script>
canvas = document.getElementById("canvas");
ctx = canvas.getContext("2d");
function Norm(xA,yA,xB,yB) {return Math.sqrt(Math.pow(xB-xA,2)+Math.pow(yB-yA,2));}
function DashedLine(xA,yA,xB,yB,L,l) {
Nhatch=Norm(xA,yA,xB,yB)/(L+l);
x1=xA;y1=yA;
for (i=0;i < Nhatch; i++) {
newXY=Hatch(xA,yA,xB,yB,x1,y1,L);
x2=newXY[0];y2=newXY[1];
ctx.beginPath();ctx.moveTo(x1,y1);ctx.lineTo(x2,y2);ctx.stroke();
newXY=Hatch(xA,yA,xB,yB,x2,y2,l);
x1=newXY[0];
y1=newXY[1];
}
}
function Hatch(xA,yA,xB,yB,x1,y1,l) {
a=(yB-yA)/(xB-xA);b=yA-a*xA;// Equation reduite y=ax+b de (AB):
if ((xB-xA)>0) {sgn=1;} else {sgn=-1;}
x2=sgn*l/Math.sqrt(1+a*a)+x1;
y2=a*x2+b;
if (Norm(x1,y1,x2,y2)>Norm(x1,y1,xB,yB)) {x2=xB;y2=yB;}
return [x2,y2];
}
// Et 4 exemples d'utilisation:
xA=10;yA=20;
xB=200;yB=50;
DashedLine(xA,yA,xB,yB,20,5);
ctx.strokeStyle = "red";ctx.lineWidth=3;
xA=10;yA=50;xB=250;yB=100;
DashedLine(xA,yA,xB,yB,20,5);
ctx.strokeStyle = "green";ctx.lineWidth=2;
xA=10;yA=160;xB=250;yB=130;
DashedLine(xA,yA,xB,yB,50,5);
ctx.strokeStyle = "blue";
xA=10;yA=180;xB=280;yB=180;
DashedLine(xA,yA,xB,yB,2,2);
</script>
- Affichage:
Détails et explications sur le code et les calculs effectués
Pour tracer cette ligne pointillée, on part du point
On cherche alors le point
On réitère ensuite en prenant
On recommence ensuite…
Cette boucle est implémentée dans la fonction DashedLine.
Il reste à déterminer les coordonnées du point
Détails de la fonction Hatch
On cherche donc les coordonnéesTout d'abord, si on connaît l'équation réduite
Equation réduite de la droite 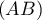
L'équation réduite s'écrit Le coefficient directeur
Ensuite, comme par exemple
On calcule ainsi simplement les coefficients
Calcul des coordonnées de 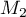
Ensuite, Or on a vu que
![\begin{array}{ll}
M_1M_2=L
&\iff \left( x_2-x_1\rp^2+\left( y_2-y_1\rp^2=L^2 \\[1em]
&\iff \left( x_2-x_1\rp^2+a^2\left( x_2-x_1\rp^2=L^2\\[1em]
&\iff \left( x_2-x_1\rp^2\left(1+a^2\rp=L^2 \\[1em]
&\iff \left( x_2-x_1\rp^2=\dfrac{L^2}{1+a^2}
\enar](canvas-line-style-pointilles-dashed-IMG/55.png)
On tourve ainsi deux possibilités pour
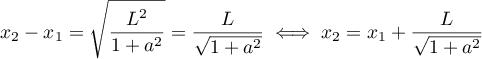
ou
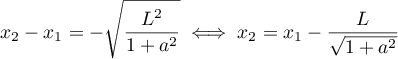
Ces deux valeurs sont les deux abscisses possibles pour
(6,1)
\rput(-1,.95){$\bullet$}\rput(-1,1.2){$A$}
\rput(1,.95){$\bullet$}\rput(1,1.2){$M_2$}
\rput(2,.95){$\bullet$}\rput(2,1.2){$M_1$}
\rput(3,.95){$\bullet$}\rput(3,1.2){$M_2$}
\rput(6,.95){$\bullet$}\rput(6,1.2){$B$}
\psline(1,1.1)(1,.1)\psline{<->}(1,.2)(2,.2)
\psline(2,1.1)(2,.1)\psline{<->}(3,.2)(2,.2)
\psline(3,1.1)(3,.1)
\rput(1.5,.4){$L$}\rput(2.5,.4){$L$}
\end{pspicture}](canvas-line-style-pointilles-dashed-IMG/60.png)
Il reste donc à choisir le point
- si
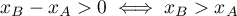 ,
, 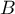 est à droite de
est à droite de 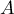 dans le
canvas, et donc aussi
dans le
canvas, et donc aussi 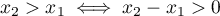 .
.
- si
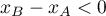 , c'est le contraire.
, c'est le contraire.
En résumé, on a:
et alors,
Dernière chose: il faut que
Voir aussi: