Dessiner une flèche / vecteur dans canvas

avec la bonne orientation !


Dans l'élément canvas de html5, on peut facilement tracer des lignes et des polygones. Pour tracer des flèches au bout de ces lignes, ou des vecteurs, il faut réfléchir un peu…
Ci-dessous une fonction qui permet de tracer des vecteurs ou des flèches.
La fonction Vecteur(xA,yA,xB,yB,ArrowLength,ArrowWidth) détaillée ci-dessous trace le vecteur $\overrightarrow{AB}, c'est-à-dire le segment $[AB] ainsi que la flèche au point $B$ orientée convenablement.
Les paramètres sont
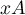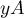  • $xA et $yA: les coordonnées de l'origine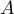 A
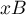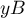  • $xA et yA: les coordonnées de l'extrémité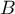 B
  • ArrowLength et ArrowWidth: deux paramètres optionnels et qui désignent deux paramètres de taille pour le dessin de la flèche, tel que représenté ci-dessous:


\psset{unit=1.2cm,linewidth=1.2pt,arrowsize=7pt} \begin{pspicture}(-.4,-.6)(6.5,4.) % \psline[arrowsize=14pt,arrowlength=2,arrowinset=1.2]{->}(1,1)(5,3) \psline(0,2)(6,2) \psline(4.2,3.4)(6,2)(4.2,0.6) \psline[linewidth=1.5pt,linestyle=dotted,linecolor=blue](4.2,3.4)(4.2,0.6) \rput(-0.1,2.2){\large$A$}\rput(0,1.97){\Large$\bullet$} \rput(6.2,2.2){\large$B$}\rput(6,1.97){\Large$\bullet$} \rput(3.9,2.2){\large$C$}\rput(4.2,1.97){\Large\blue$\bullet$} \rput(4.2,3.6){\large$D$}\rput(4.2,3.37){\Large\blue$\bullet$} \rput(4.2,.3){\large$E$}\rput(4.2,.57){\Large\blue$\bullet$} % \psline{<->}(3.6,2.1)(3.6,3.5)\rput{90}(3.3,2.8){\small ArrowWidth} \psline{<->}(3.6,1.9)(3.6,.5)\rput{90}(3.3,1.2){\small ArrowWidth} \psline{<->}(4.2,-0.2)(6,-.2)\rput(5.1,-.45){\small ArrowLength} \end{pspicture}


Pour les impatients ou les personnes allergiques au calcul, vectoriel entre autre, ou encore qui n'éprouvent pas le besoin de comprendre le fonctionnement d'une telle fonction (et qui ne pensent donc pas non plus avoir besoin de l'adapter un jour à une autre fin un peu différente), le code complet et son illustration se trouve un peu plus bas.
Un peu d'analyse vectorielle permet de déterminer simplement les coordonnées des points C, D et E.
Tous les détails sur le calcul vectoriel se trouvent Télécharger et pour le produit scalaire: Télécharger.

Coordonnées du point C  
Les vecteurs $\overrightarrow{BC} et $\overrightarrow{BA} sont colinéaires de même sens, le vecteur $\dfrac{\overrightarrow{BA}}{AB} étant de plus unitaire (de longueur, ou norme, égale à 1).

La fonction Norm(xA,yA,xB,yB) calcule et retourne justement la longueur $AB.
On a ainsi   $\overrightarrow{BC}=\text{ArrowLength}\tm\dfrac{\overrightarrow{BA}}{AB},   ce qui s'écrit en termes de coordonnées:
\la\begin{array}{lcl} xC-xB&=&\text{ArrowLength}\tm\dfrac{xB-xA}{AB}\\[.4cm] yC-yB&=&\text{ArrowLength}\tm\dfrac{yB-yA}{AB}\\ \enar\right.

soit encore,
\la\begin{array}{lcl} xC&=&xB+\text{ArrowLength}\tm\dfrac{xB-xA}{AB}\\[.4cm] yC&=&yB+\text{ArrowLength}\tm\dfrac{yB-yA}{AB}\\ \enar\right.



Coordonnées du point D  
Les droites $(AB) et $(DC) sont perpendiculaires; en d'autres termes, plus efficaces pour mener des calculs analytiques, les vecteurs $\overrightarrow{DC} et $\overrightarrow{AB} sont orthogonaux.
 
Un vecteur orthogonal au vecteur $\overrightarrow{AB}\lp\begin{array}{l} xB-xA\\[.2cm] yB-yA\enar\rp est le vecteur $\vec{u}\lp\begin{array}{l} -\lp yB-yA\rp\\[.2cm] \quad xB-xA\enar\rp.
(pour lequel on vérifie bien simplement que le produit scalaire $\overrightarrow{AB}\cdot\vec{u}=0 ).

Ainsi, comme de plus le vecteur $\vec{u} et $\overrightarrow{AB} on a la même norme: $\|\vec{u}\|=\|\overrightarrow{AB}\|=AB, et de plus on a $\overrightarrow{CD}=ArrowWidth\tm\dfrac{\vec{u}}{AB}, soit, en termes de coordonnées:
\la\begin{array}{lcl} xD-xC&=&\text{ArrowWidth}\tm\dfrac{-\left( yB-yA\rp}{AB}\\[.4cm] yD-yC&=&\text{ArrowWidth}\tm\dfrac{xB-xA}{AB}\\ \enar\right.

soit encore,
\la\begin{array}{lcl} xD&=&xC+\text{ArrowWidth}\tm\dfrac{-\left( yB-yA\rp}{AB}\\[.4cm] yD&=&yC+\text{ArrowWidth}\tm\dfrac{xB-xA}{AB}\\ \enar\right.



Coordonnées du point E  

De même que pour le point D, on a: $\overrightarrow{CE}=ArrowWidth\tm\dfrac{-\vec{u}}{AB}, soit en termes de coordonnées:
\la\begin{array}{lcl} xE&=&xC-\text{ArrowWidth}\tm\dfrac{-\left( yB-yA\rp}{AB}\\[.4cm] yE&=&yC-\text{ArrowWidth}\tm\dfrac{xB-xA}{AB}\\ \enar\right.



Représentation graphique Une fois les coordonnées de ces points calculées, il ne reste plus qu'à tracer, en commençant par ctx.beginPath(); puis,
  • le segment $[AB]: ctx.moveTo(xA,yA);ctx.lineTo(xB,yB);
  • la flèche 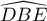$\widehat{DBE}: ctx.moveTo(xD,yD);ctx.lineTo(xB,yB);ctx.lineTo(xE,yE);
et enfin, on relie les points: ctx.stroke(); 
<canvas id="canvas" width="300" height="200" ></canvas>

<script>
Width=document.getElementById("canvas").width; 
Height=document.getElementById("canvas").height; 
canvas = document.getElementById("canvas"); 
ctx = canvas.getContext("2d"); 
 
function Norm(xA,yA,xB,yB) {
  return Math.sqrt(Math.pow(xB-xA,2)+Math.pow(yB-yA,2));
} 
function Vecteur (xA,yA,xB,yB,ArrowLength,ArrowWidth) { 
  if (ArrowLength === undefined) {ArrowLength=10;} 
  if (ArrowWidth === undefined) {ArrowWidth=8;} 
  ctx.lineCap="round"; 
// Calculs des coordonnées des points C, D et E 
  AB=Norm(xA,yA,xB,yB); 
  xC=xB+ArrowLength*(xA-xB)/AB;yC=yB+ArrowLength*(yA-yB)/AB; 
  xD=xC+ArrowWidth*(-(yB-yA))/AB;yD=yC+ArrowWidth*((xB-xA))/AB; 
  xE=xC-ArrowWidth*(-(yB-yA))/AB;yE=yC-ArrowWidth*((xB-xA))/AB; 
  // et on trace le segment [AB], et sa flèche: 
  ctx.beginPath(); 
  ctx.moveTo(xA,yA);ctx.lineTo(xB,yB); 
  ctx.moveTo(xD,yD);ctx.lineTo(xB,yB);ctx.lineTo(xE,yE); 
  ctx.stroke(); 
} 
 
// Et 3 exemples d'utilisation: 
ctx.strokeStyle="red"; 
Vecteur(30,180,120,150); 
 
ctx.strokeStyle="blue"; 
ctx.lineWidth=4; 
ArrowLength=10;ArrowWidth=8; 
Vecteur(200,100,30,25,ArrowLength,ArrowWidth); 
 
ctx.strokeStyle="green"; 
ctx.lineWidth=2; 
ArrowLength=6;ArrowWidth=4; 
for (i=0;i<15;i++) { 
  Vecteur(240,30+10*i,260,20+10*i,ArrowLength,ArrowWidth); 
}
</script>
Voir aussi:


LongPage: h2: 1 - h3: 0