Suite récurrente et algorithmique

Bac S - Liban 2013

1. On souhaite écrire un algorithme affichant, pour un entier naturel donné, tous les termes de la suite, du rang au rang . Parmi les trois algorithmes suivants, un seul convient. Préciser lequel en justifiant la réponse.
   

   Algorithme no1
   Variables: v est un réel i et n sont des entiers naturels Début de l'algorithme: Lire n v prend la valeur 1 Pour i variant de 1 à n faire     v prend la valeur 9 6-v Fin pour Afficher v
   Fin algorithme

   Algorithme no2
   Variables: v est un réel i et n sont des entiers naturels Début de l'algorithme: Lire n Pour i variant de 1 à n faire v prend la valeur 1     v prend la valeur 9 6-v Fin pour Afficher v
   Fin algorithme

   Algorithme no3
   Variables: v est un réel i et n sont des entiers naturels Début de l'algorithme: Lire n v prend la valeur 1 Pour i variant de 1 à n faire     Afficher v     v prend la valeur 9 6-v Fin pour Afficher v
   Fin algorithme
2. Pour , on obtient l'affichage suivant :
   
   
   
   
   
   Pour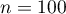 , les derniers termes affichés sont :
   
   
   
   
   Quelles conjectures peut-on émettre concernant la suite ?
   
    
3. 1. Démontrer par récurrence que, pour tout entier naturel ,
      .
   2. Démontrer que, pour tout entier naturel ,
      .
      La suite est-elle monotone ?
      
   3. Démontrer que la suite est convergente.

Partie B - Recherche de la limite de la suite

1. Démontrer que est une suite arithmétique de raison
   
2. En déduire l'expression de , puis celle de en fonction de .
   
3. Déterminer la limite de la suite .