Tortues des Galapagos
Colle de mathématiques
Sujet de colle de maths:- Couples de variables aléatoiresCouples de variables aléatoires
Énoncé du sujet
Soit 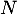 un entier naturel non nul.
un entier naturel non nul.
Une tortue des Galapagos pond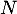 oeufs qu'elle enfouit dans le sable d'une île.
Les oeufs ont (indépendamment les uns des autres) une probabilité
oeufs qu'elle enfouit dans le sable d'une île.
Les oeufs ont (indépendamment les uns des autres) une probabilité ![$p\in]0, 1[$](/Generateur-Devoirs/Colles/CVA/TG/3.png) d'éclore et les bébés tortues qui naissent ont (de manière indépendante) une probabilité q d'être des bébés tortues mâles.
On pose
d'éclore et les bébés tortues qui naissent ont (de manière indépendante) une probabilité q d'être des bébés tortues mâles.
On pose 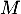 la variable aléatoire désignant le nombre de bébés tortues mâles qui naissent et
la variable aléatoire désignant le nombre de bébés tortues mâles qui naissent et 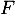 le nombre de tortues femelles qui naissent.
le nombre de tortues femelles qui naissent.
Une tortue des Galapagos pond
- Donner les lois des variables
 ,
, 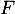 ,
,  .
.
-
- Les variables
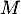 et
et  sont-elles indépendantes ?
sont-elles indépendantes ?
- Calculer la covariance de
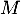 et
et 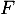 .
.
- Les variables
- On pose maintenant
 suivant une loi de Poisson de paramètre
suivant une loi de Poisson de paramètre 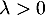 .
Les autres hypothèses restent inchangées.
.
Les autres hypothèses restent inchangées.
- Calculer la loi de
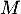 .
.
- Calculer la covariance de
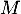 et
et 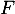 .
.
- Les variables aléatoires
 et
et  sont-elles indépendantes ?
sont-elles indépendantes ?
- Calculer la loi de
Correction
Correction
Oral ENSAE - Saclay - 2019- Un bébé mâle nait avec la probailité
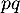 .
.
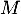 est égal au nombre de succès (bébé mâle) dans une répétition de
est égal au nombre de succès (bébé mâle) dans une répétition de 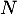 expériences aléatoires indépendantes.
expériences aléatoires indépendantes.
La loi de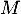 est donc la loi binomiale de paramètres
est donc la loi binomiale de paramètres 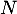 et
et 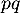 .
.
De même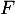 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres 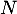 et
et  .
.
Enfin,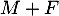 désigne le nombre d'œ ufs qui éclosent, et suit donc la loi binomiale de paramètres
désigne le nombre d'œ ufs qui éclosent, et suit donc la loi binomiale de paramètres 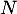 et
et 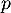 .
.
-
- Les variables
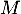 et
et 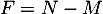 ne sont pas indépendantes.
Par exemple,
ne sont pas indépendantes.
Par exemple,
![\[P(M=N\cap F=N)=0\not=P(M=N)\,P(F=N)\]](/Generateur-Devoirs/Colles/CVA/TG_c/15.png)
-
![\[cov(M,F)=\dfrac12\left( V(M+F)-V(F)-V(M)\rp\]](/Generateur-Devoirs/Colles/CVA/TG_c/16.png)
où
![\[\begin{array}{lcl}
V(M+F)&=&Np(1-p)\\
V(F)&=&Np(1-q)(1-p(1-q))\\
V(M)&=&Npq(1-pq)
\enar\]](/Generateur-Devoirs/Colles/CVA/TG_c/17.png)
- Les variables
-
- On a alors
![\[\begin{array}{lcl}P(M=k)&=&\dsp\sum_{n=0}^{+\infty} P(N=n\cap M=k)\\
&=&\dsp\sum_{n=k}^{+\infty} P(N=n\cap M=k)\\
&=&\dsp\sum_{n=k}^{+\infty} P(M=k|N=n)\,P(N=n) \\
&=&\dsp\sum_{n=k}^{+\infty}\binom{n}{k}(pq)^k(1-pq)^{n-k}\dfrac{e^{-\lambda}\lambda^n}{n!}\\
&=&\displaystyle e^{-\lambda}\left( pq\rp^k\sum_{n=k}^{+\infty}
\dfrac{\lambda^n(1-pq)^{n-k}}{k!(n-k)!}\\[1.6em]
&=&\displaystyle e^{-\lambda}\dfrac{\left( pq\rp^k}{k!\lambda^k}
\sum_{n=k}^{+\infty}
\dfrac{\bigl(\lambda(1-pq)\bigr)^{n-k}}{(n-k)!}\\[1.6em]
\enar\]](/Generateur-Devoirs/Colles/CVA/TG_c/18.png)
soit, en effectuant un changement d'indice dans la somme pour faire apparaître la série exponentielle:
![\[\begin{array}{lcl}P(M=k)&=&
\displaystyle e^{-\lambda}\dfrac{\lp\lambda pq\rp^k}{k!}
\sum_{n=0}^{+\infty}
\dfrac{\bigl(\lambda(1-pq)\bigr)^n}{n!}\\[1.6em]
&=&\displaystyle e^{-\lambda}\dfrac{\lp\lambda pq\rp^k}{k!}
e^{\lambda(1-pq)}\\
&=&e^{-\lambda pq}\dfrac{\lp\lambda pq\rp^k}{k!}
\enar\]](/Generateur-Devoirs/Colles/CVA/TG_c/19.png)
qui est l'expression d'une loi de Poisson de paramètre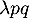 .
.
- Pour la loi de Poisson de paramètre
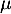 , l'espérance et la variance sont égales à
, l'espérance et la variance sont égales à 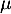 .
.
La variable aléatoire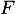 suit aussi une loi de Poisson de paramètre
suit aussi une loi de Poisson de paramètre
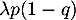 , et la variable
, et la variable 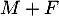 est de paramètre
est de paramètre  ,
d'où
,
d'où
![\[\begin{array}{lcl}cov(M,F)&=&\dfrac12\bigl( V(M+F)-V(F)-V(M)\bigr)\\[1em]
&=&\dfrac12\bigl( \lambda p-\lambda p(1-q)-\lambda pq \bigr)
=0
\enar\]](/Generateur-Devoirs/Colles/CVA/TG_c/27.png)
- Pour deux entiers
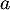 et
et 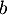 , on a
, on a
![\[\begin{array}{lcl}P(M=a\cap F=b)
&=&\dsp\sum_{n=a+b}^{+\infty}P(M=a\cap F=b\cap N=n)\\
&&\hspace*{-8em}=\dsp\sum_{n=a+b}^{+\infty}P(M=a\cap F=b | N=n)\,P(N=n)\\
&&\hspace*{-8em}=\dsp\sum_{n=a+b}^{+\infty}P(M=a)P(F=b|M=a)\,P(N=n)\\
&&\hspace*{-8em}=\dsp\sum_{n=a+b}^{+\infty}
\binom{n}{a}(pq)^a(1-pq)^{n-a}
\binom{n-a}{b}(p(1-q))^b(1-p(1-q))^{n-a-b}
\dfrac{e^{-\lambda}\lambda^n}{n!} \\
&&\hspace*{-8em}=
e^{-\lambda}(pq)^a(p(1-q))^b\dfrac{\lambda^{a+b}}{a!\,b!}
\dsp\sum_{n=a+b}^{+\infty}
\dfrac{(1-p(1-q))^{n-a-b}\lambda^{n-a-b}}{(n-a-b)!}\\
&&\hspace*{-8em}=
e^{-\lambda}(pq)^a(p(1-q))^b\dfrac{\lambda^{a+b}}{a!\,b!}
e^{\lambda(1-p(1-q))}
\enar\]](/Generateur-Devoirs/Colles/CVA/TG_c/30.png)
Par ailleurs, d'après 3.a),
![\[\begin{array}{lcl}P(M=a)P(F=b)
&=&e^{-\lambda pq}\dfrac{\lp\lambda pq\rp^a}{a!}
e^{-\lambda p(1-q)}\dfrac{\lp\lambda p(1-q)\rp^b}{b!}\\[1em]
&=&e^{-\lambda p}(\lambda p)^{a+b}\dfrac{q^a(1-q)^b}{a!\,b!}
\enar\]](/Generateur-Devoirs/Colles/CVA/TG_c/31.png)
ce qui montre maintenant que les variables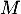 et
et 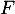 sont indépendantes.
sont indépendantes.
- On a alors
Tag:Couples de variables aléatoires
Autres sujets au hasard:
