Système d'équations différentielles
Colle de mathématiques
Sujet de colle de maths:- Équation différentielleÉquation différentielle
- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
Énoncé du sujet
Résoudre le système d'équations différentielles:
![\[\la\begin{array}{ll}
x'=2x-y\\[.6em]
y'=-x+2y\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff/1.png)
avec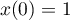 et
et 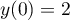 .
.
![\[\la\begin{array}{ll}
x'=2x-y\\[.6em]
y'=-x+2y\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff/1.png)
avec
Correction
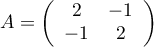 et
et 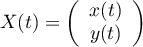 ,
alors
,
alors 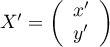 et le système s'écrit
et le système s'écrit
 .
.
On sait alors que la solution de cette équation différentielle est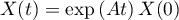 .
.
Il reste donc à calculer l'exponentielle de matrice:
![\[\exp(At)=\sum_{n\geqslant0}\dfrac{(At)^n}{n!}
=\sum_{n\geqslant0}\dfrac1{n!}A^nt^n\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/6.png)
et donc les puissances de la matrice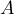 .
.
On peut à cette fin diagonaliser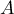 (qui est une matrice symétrique réelle,
donc en particulier bien diagonalisable).
(qui est une matrice symétrique réelle,
donc en particulier bien diagonalisable).
Le polynôme caractéristique de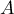 est
est
![\[\begin{array}{ll}
\chi_A(X)&=\det(XI-A)=\left|\begin{array}{cc}X-2 & 1\\1 & X-2\enar\right| \\[1.2em]
&=(X-2)^2-1^2=(X-1)(X-3)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/10.png)
Ainsi,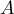 admet deux valeurs propres 1 et 3.
admet deux valeurs propres 1 et 3.
Sous-espace propre associé à la valeur propre 1: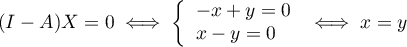 .
Le sous-espace propre est de dimension 1, engendré par
.
Le sous-espace propre est de dimension 1, engendré par
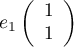 .
.
Sous-espace propre associé à la valeur propre 3: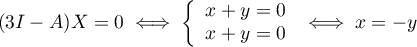 .
Le sous-espace propre est de dimension 1, engendré par
.
Le sous-espace propre est de dimension 1, engendré par
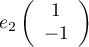 .
.
On a alors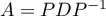 avec la matrice diagonale
avec la matrice diagonale
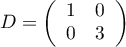 et la matrice de passage
et la matrice de passage
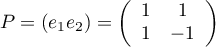 et son inverse
et son inverse
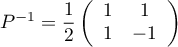 .
.
On obtient alors,
![\[\begin{array}{ll}
A^n&=\left( PDP^{-1}\rp^n \\[.5em]
&= PDP^{-1}\,PDP^{-1}\,\dots PDP^{-1}\\[.5em]
&=PD^nP^{-1} \\[.5em]
&=\lp\begin{array}{cc}1&1\\1&-1\enar\right)
\lp\begin{array}{cc}1&0\\0&3^n\enar\right)
\dfrac12\lp\begin{array}{cc}1&1\\1&-1\enar\right) \\[1em]
&=\dfrac12\lp\begin{array}{cc}1+3^n & 1-3^n\\1-3^n&1+3^n \enar\rp\\[1em]
&=\dfrac12E+3^nF
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/20.png)
avec les matrices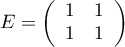 et
et 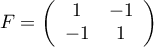
On trouve alors enfin,
![\[\begin{array}{ll}\exp(At)
&=\dsp\sum_{n\geqslant0}\dfrac1{n!}A^nt^n \\[1.4em]
&=\dsp\sum_{n\geqslant0}\dfrac{t^n}{n!}\lp\dfrac12E+3^nF\right) \\[1.6em]
&=\dsp\lp\sum_{n\geqslant0}\dfrac{t^n}{n!}\rp\dfrac12E
+\lp\sum_{n\geqslant0}\dfrac{3^nt^n}{n!}\right) F \\[1.6em]
&=\dfrac12e^tE+e^{3t}F
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/23.png)
puis en revenant aux solutions du système différentiel: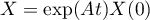 avec
avec 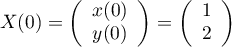 ,
donc
,
donc
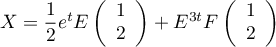 soit finalement,
soit finalement,
![\[\la\begin{array}{ll}
x(t)&=\dfrac32e^t-e^{3t}\\
y(t)&=\dfrac32e^t+e^{3t}
\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/27.png)
Correction
On poseOn sait alors que la solution de cette équation différentielle est
Il reste donc à calculer l'exponentielle de matrice:
![\[\exp(At)=\sum_{n\geqslant0}\dfrac{(At)^n}{n!}
=\sum_{n\geqslant0}\dfrac1{n!}A^nt^n\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/6.png)
et donc les puissances de la matrice
On peut à cette fin diagonaliser
Le polynôme caractéristique de
![\[\begin{array}{ll}
\chi_A(X)&=\det(XI-A)=\left|\begin{array}{cc}X-2 & 1\\1 & X-2\enar\right| \\[1.2em]
&=(X-2)^2-1^2=(X-1)(X-3)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/10.png)
Ainsi,
Sous-espace propre associé à la valeur propre 1:
Sous-espace propre associé à la valeur propre 3:
On a alors
On obtient alors,
![\[\begin{array}{ll}
A^n&=\left( PDP^{-1}\rp^n \\[.5em]
&= PDP^{-1}\,PDP^{-1}\,\dots PDP^{-1}\\[.5em]
&=PD^nP^{-1} \\[.5em]
&=\lp\begin{array}{cc}1&1\\1&-1\enar\right)
\lp\begin{array}{cc}1&0\\0&3^n\enar\right)
\dfrac12\lp\begin{array}{cc}1&1\\1&-1\enar\right) \\[1em]
&=\dfrac12\lp\begin{array}{cc}1+3^n & 1-3^n\\1-3^n&1+3^n \enar\rp\\[1em]
&=\dfrac12E+3^nF
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/20.png)
avec les matrices
On trouve alors enfin,
![\[\begin{array}{ll}\exp(At)
&=\dsp\sum_{n\geqslant0}\dfrac1{n!}A^nt^n \\[1.4em]
&=\dsp\sum_{n\geqslant0}\dfrac{t^n}{n!}\lp\dfrac12E+3^nF\right) \\[1.6em]
&=\dsp\lp\sum_{n\geqslant0}\dfrac{t^n}{n!}\rp\dfrac12E
+\lp\sum_{n\geqslant0}\dfrac{3^nt^n}{n!}\right) F \\[1.6em]
&=\dfrac12e^tE+e^{3t}F
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/23.png)
puis en revenant aux solutions du système différentiel:
![\[\la\begin{array}{ll}
x(t)&=\dfrac32e^t-e^{3t}\\
y(t)&=\dfrac32e^t+e^{3t}
\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/exSysEqDiff_c/27.png)
Tags:Équation différentielleDiagonalisation
Autres sujets au hasard:

Voir aussi: