Sur l'espérance d'une variable aléatoire
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires discrètesVariables aléatoires discrètes
Énoncé du sujet
Oral ESCP, BL - 2021
- Soit
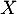 une variable aléatoire à valeurs dans
une variable aléatoire à valeurs dans 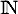 , définie sur un espace probabilisé
, définie sur un espace probabilisé 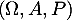 .
.
- Montrer que, pour tout
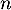 de
de 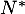 , on a:
, on a:
![\[\sum_{k=0}^nkP(X=k) = \sum_{k=0}^{n-1}P(X>k)-nP(X>n)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4/6.png)
- On suppose que la série
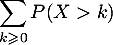 converge.
Démontrer que
converge.
Démontrer que 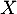 admet une espérance.
admet une espérance.
- Réciproquement, on suppose que
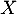 admet une espérance.
admet une espérance.
Démontrer que la suite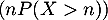 tend vers 0,
puis que la série
tend vers 0,
puis que la série 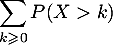 converge et enfin que
converge et enfin que
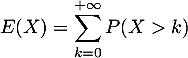
- Montrer que, pour tout
- Une application: soit
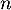 et
et 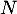 deux entiers non nuls.
On dispose d'une urne qui contient
deux entiers non nuls.
On dispose d'une urne qui contient 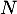 boules indiscernables au toucher numérotées de 1 à
boules indiscernables au toucher numérotées de 1 à 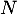 . On effectue dans cette urne,
. On effectue dans cette urne, 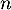 tirages successifs avec remise d'une boule et on note
tirages successifs avec remise d'une boule et on note 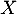 le plus grand nombre obtenu.
le plus grand nombre obtenu.
- Soit
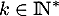 . Déterminer
. Déterminer 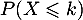 . En déduire la loi de
. En déduire la loi de 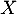 .
.
- À l'aide des questions précédentes, déterminer l'espérance de
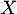 en fonction de
en fonction de 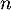 et
et 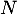 .
.
- Soit
Correction
Correction
Oral ESCP, BL - 2021-
- On se ramène à des inégalités strictes:
![\[P(X=k)=P(X>k-1)-P(X>k)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/1.png)
et donc
![\[\begin{array}{ll}\dsp\sum_{k=0}^nkP(X=k)&=\dsp\sum_{k=1}^nkP(X=k)\\
&=\dsp\sum_{k=1}^nk\biggl(P(X>k-1)-P(X>k)\biggr)\\
&=\dsp\sum_{k=1}^nkP(X>k-1)-\sum_{k=1}^nkP(X>k)\\
&=\dsp\sum_{k=0}^{n-1}(k+1)P(X>k)-\sum_{k=1}^nkP(X>k)\\
&=\dsp\sum_{k=1}^{n-1}P(X>k)+P(X>0)-nP(X>n)\\
&=\dsp\sum_{k=0}^{n-1}P(X>k)-nP(X>n)
\enar\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/2.png)
- D'après le résultat précédent, on a donc
![\[0\leqslant \sum_{k=0}^nkP(X=k)\leqslant\sum_{k=0}^{n-1}P(X>k)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/3.png)
et donc, puisqu'on suppose la série de droite convergente,
![\[0\leqslant \sum_{k=0}^nkP(X=k)\leqslant\sum_{k=0}^{+\infty}P(X>k)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/4.png)
Ainsi, la suite des sommes partielles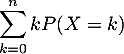 est majorée.
Comme elle est croissante (somme de termes positifs), on en déduit qu'elle converge, ce qui signifie exactement que l'expérance est une série convergente, et existe donc bien.
est majorée.
Comme elle est croissante (somme de termes positifs), on en déduit qu'elle converge, ce qui signifie exactement que l'expérance est une série convergente, et existe donc bien.
- On a
![\[nP(X>n)=n\sum_{k=n+1}^{+\infty}P(X=k)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/6.png)
On fait alors intervenir la série exprimant l'espérance
![\[\begin{array}{ll}nP(X>n)&=\sum_{k=n+1}^{+\infty}nP(X=k)\\
&\leqslant kP(X=k)\enar\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/7.png)
Le terme de droite est alors le reste de la série donnant l'espérance, donc le reste d'une série convergente: il tend donc vers 0, comme le terme positif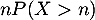 .
.
On a alors, d'après l'égalité démontré au début,
![\[\sum_{k=0}^{n-1}P(X>k)=\sum_{k=0}^nkP(X=k)+nP(X>n)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/9.png)
La somme de droite est supposée converger (vers l'expérance) et le deuxième tend vers 0 comme on vient de le montrer. La série de gauche converge donc aussi.
Enfin, par passage à la limite dans l'égalité précédente, on obtient bien
![\[E(X)=\dsp\sum_{k=0}^{+\infty}P(X>k)\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/10.png)
- On se ramène à des inégalités strictes:
-
- Les tirages ont indépendants les uns des autres puisqu'il y a remise après chaque tirage.
La probabilité que pour un tirage on tire une boule avec un numéro inférieur ou égal à
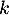 est
est 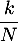 .
.
Par indépendance des tirages, on a alors
![\[P(X\leqslant k)=\lp\dfrac{k}N\rp^n\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/13.png)
On en déduit la loi de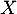 par
par
![\[\begin{array}{ll}P(K=k)&=P(X\leqslant k)-P(X\leqslant k-1)\\
&=\lp\dfrac{k}N\rp^n-\lp\dfrac{k-1}N\rp^n\enar\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/15.png)
- Pour utiliser les résultats de la partie précédente, on écrit tout d'abord
![\[P(X>k)=1-P(X\leqslant k)=1-\lp\dfrac{k}N\rp^n\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/16.png)
puis
![\[\begin{array}{ll}E(X)&=\dsp\sum_{k=0}^{+\infty}P(X>k)\\
&=\dsp\sum_{k=0}^{N-1}\lp1-\lp\dfrac{k}N\rp^n\rp\enar\]](/Generateur-Devoirs/Colles/VAD/ESCP-BL-2021-4.4_c/17.png)
- Les tirages ont indépendants les uns des autres puisqu'il y a remise après chaque tirage.
La probabilité que pour un tirage on tire une boule avec un numéro inférieur ou égal à
Tag:Variables aléatoires discrètes
Autres sujets au hasard:

Voir aussi: