Suite definie par une integrale généralisée
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
On définit la suite  par :
par :
![\[u_n=\dsp\int_0^{+\infty} \dfrac{e^{-x}}{x+\frac{1}{n}} dx\]](/Generateur-Devoirs/Colles/Integrale/stint/2.png)
![\[u_n=\dsp\int_0^{+\infty} \dfrac{e^{-x}}{x+\frac{1}{n}} dx\]](/Generateur-Devoirs/Colles/Integrale/stint/2.png)
- Justifier que la suite
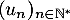 est bien définie et étudier son sens de variation.
est bien définie et étudier son sens de variation.
- On définit, pour tout
 ,
,
![\[v_n=\dsp\int_0^{1} \dfrac{e^{-x}}{x+\frac{1}{n}} dx \quad \text{ et }\quad w_n=\displaystyle\int_1^{+\infty} \dfrac{e^{-x}}{x+\frac{1}{n}} dx \]](/Generateur-Devoirs/Colles/Integrale/stint/5.png)
Montrer que, pour tout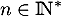 :
:
![\[v_n\geq \dfrac{\ln(n+1)}{e}\quad\text{ et }\quad 0\leq w_n\leq \dfrac{1}{e}\]](/Generateur-Devoirs/Colles/Integrale/stint/7.png)
- Donner la limite de la suite
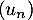 .
.
- On cherche maintenant à obtenir un résultat plus précis.
- Montre que l'intégrale
 est convergente.
est convergente.
- Montrer que pour tout
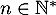 :
:
![\[0\leq \dsp\int_0^{1} \dfrac{1-e^{-x}}{x+\frac{1}{n}} dx \leq I\]](/Generateur-Devoirs/Colles/Integrale/stint/11.png)
- En déduire que :
![\[\lim\limits_{\substack{n \rightarrow +\infty }}
\dfrac{u_n}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/Integrale/stint/12.png)
- Montre que l'intégrale
Correction
Correction
Oral ENS ULM - 2021- La fonction a intégrer est continue sur
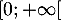 par composition et quotient de fonctions continues et il reste donc seulement à vérifier la convergence de l'intégrale n
par composition et quotient de fonctions continues et il reste donc seulement à vérifier la convergence de l'intégrale n  .
.
Pour tout entier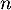 non nul, et tout
non nul, et tout 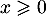 , on a, par croissances comparées,
, on a, par croissances comparées,
![\[\lim_{x\to+\infty}x^2\dfrac{e^{-x}}{x+\frac{1}{n}}=0\]](/Generateur-Devoirs/Colles/Integrale/stint_c/5.png)
c'est-à-dire que, en ,
,
![\[\dfrac{e^{-x}}{x+\frac{1}{n}}=o\lp\dfrac1{x^2}\rp\]](/Generateur-Devoirs/Colles/Integrale/stint_c/7.png)
et donc, par comparaison avec une intégrale de Riemann convergente, notre intégrale converge aussi en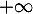 , ce qui signifie aussi
que la suite
, ce qui signifie aussi
que la suite 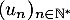 est bien définie.
est bien définie.
Pour tout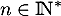 et tout
et tout 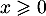 on a
on a
![\[\begin{array}{ll}
n+1>n\quad &\implies \quad 0< x+\dfrac{1}{n+1}< x+\dfrac{1}{n} \\[1.2em]
&\implies \dfrac1{x+\dfrac{1}{n+1}}<\dfrac1{x+\dfrac{1}{n}} \\[2.4em]
&\implies \dfrac{e^{-x}}{ x+\frac{1}{n+1}} >\dfrac{e^{-x}}{ x+\frac{1}{n}}
\enar\]](/Generateur-Devoirs/Colles/Integrale/stint_c/12.png)
d'où par positivité d'intégrales impropres convergentes:
![\[u_{n+1}>u_n\]](/Generateur-Devoirs/Colles/Integrale/stint_c/13.png)
c'est-à-dire que la suite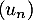 est strictement croissante
est strictement croissante
- Avec les mêmes arguments que précédemment, les suites
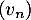 et
et 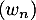 sont bien définies.
sont bien définies.
Puis, pour tout![$x\in[0,1] $](/Generateur-Devoirs/Colles/Integrale/stint_c/17.png) on a, par croissance de l'exponentielle,
on a, par croissance de l'exponentielle,
 et ainsi
et ainsi
![\[ \dfrac{1}{e(x+\frac{1}{n})} \leq \dfrac{e^{-x}}{x+\frac{1}{n}} \]](/Generateur-Devoirs/Colles/Integrale/stint_c/19.png)
d'où par positivité de l'intégrale :
![\[\dsp\int_0^1 \dfrac{1}{e(x+\frac{1}{n})} dx \leq v_n \]](/Generateur-Devoirs/Colles/Integrale/stint_c/20.png)
or
![\[\begin{array}{ll}\dsp\int_0^1 \dfrac{1}{e(x+\frac{1}{n})} dx
&= \dfrac1e\left[ \ln\left( x+\dfrac1n\right) \rb_0^1\\[1.2em]
&= \dfrac1e \left( \ln\left( 1+\dfrac{1}{n}\right) - \ln\left(\dfrac1n \right) \right) \\[1.4em]
&= \dfrac1e\ln\lp\left(1+\dfrac{1}{n} \rp\times n \rp\\[1.2em]
&= \dfrac{1}{e}\ln(n+1)
\enar\]](/Generateur-Devoirs/Colles/Integrale/stint_c/21.png)
et donc, pour tout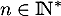
![\[v_n\quad \geq \quad \dfrac{1}{e}\ln(n+1)\]](/Generateur-Devoirs/Colles/Integrale/stint_c/23.png)
Par ailleurs pour tout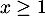 et tout
et tout 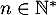 on a
on a 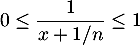 .
.
Ainsi par produit avec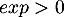 :
:
![\[0\leq \dfrac{e^{-x}}{x+\frac{1}{n}} \leq e^{-x} \]](/Generateur-Devoirs/Colles/Integrale/stint_c/28.png)
d'où par positivité des intégrales convergentes :
![\[0\leq \dsp\int_1^{+\infty} \dfrac{e^{-x}}{x+\frac{1}{n}} dx \leq\int_1^{+\infty} e^{-x}dx=\dfrac1e\]](/Generateur-Devoirs/Colles/Integrale/stint_c/29.png)
Donc, pour tout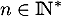 ,
,
![\[0\leqslant w_n\quad \leq \quad \dfrac{1}{e}\]](/Generateur-Devoirs/Colles/Integrale/stint_c/31.png)
- Comme
 alors par comparaison, on obtient
alors par comparaison, on obtient
![\[\lim_{n\to+\infty} v_n=+\infty\]](/Generateur-Devoirs/Colles/Integrale/stint_c/33.png)
Par ailleurs, on a vu que est bornée, et donc, en ajoutant ce s deux suites,
est bornée, et donc, en ajoutant ce s deux suites,
![\[\lim_{n\to+\infty}u_n=\lim_{n\to+\infty} (v_n+w_n ) = +\infty\]](/Generateur-Devoirs/Colles/Integrale/stint_c/35.png)
-
- La fonction
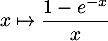 est continue sur
est continue sur ![$]0,1]$](/Generateur-Devoirs/Colles/Integrale/stint_c/37.png) ( composition, différence et quotient de fonctions continues ) et est non définie en 0 donc l'intégrale
( composition, différence et quotient de fonctions continues ) et est non définie en 0 donc l'intégrale  est impropre en 0, et uniquement en 0.
est impropre en 0, et uniquement en 0.
Puis comme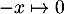 en 0 alors par équivalents usuels :
en 0 alors par équivalents usuels :
![\[\dfrac{1-e^{-x}}{x}\underset{0}{\sim} -\dfrac{(-x)}{x} = 1\]](/Generateur-Devoirs/Colles/Integrale/stint_c/40.png)
ainsi :
![\[\lim_{x\to0} \dfrac{1-e^{-x}}{x} = 1\]](/Generateur-Devoirs/Colles/Integrale/stint_c/41.png)
c'est-à-dire que la fonction à intégrée est en fait prolongeable par continuuité en 0, et donc l'intégrale en 0 est bien définie.
Finalement, l'intégrale existe bien.
- On a
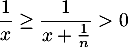 pour tout
pour tout ![$x\in]0,1]$](/Generateur-Devoirs/Colles/Integrale/stint_c/43.png) et tout
et tout 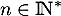 .
Par ailleurs comme pour tout réel
.
Par ailleurs comme pour tout réel ![$x\in]0,1]$](/Generateur-Devoirs/Colles/Integrale/stint_c/45.png) on a par stricte monotonie de l'exponentielle que
on a par stricte monotonie de l'exponentielle que 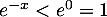 , alors par produit puis positivité d'intégrales convergentes :
, alors par produit puis positivité d'intégrales convergentes :
![\[0\leq \displaystyle\int_0^1 \dfrac{1-e^{-x}}{x+\frac{1}{n}}dx \leq I
\]](/Generateur-Devoirs/Colles/Integrale/stint_c/47.png)
- Après calculs on trouve, par linéarité appliquée à une intégrale convergente :
![\[\int_0^1 \dfrac{1-e^{-x}}{x+\frac{1}{n}}dx = \ln(n+1)-v_n \]](/Generateur-Devoirs/Colles/Integrale/stint_c/48.png)
d'où d'après b) :
![\[\ln(n+1)-I\leq v_n\leq \ln(n+1)\]](/Generateur-Devoirs/Colles/Integrale/stint_c/49.png)
ou encore, comme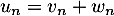 ,
,
![\[\ln(n+1)-I+w_n\leq u_n\leq \ln(n+1)+w_n\]](/Generateur-Devoirs/Colles/Integrale/stint_c/51.png)
et donc,
![\[\dfrac{\ln(n+1)}{\ln(n)}+\dfrac{-I+w_n}{\ln(n)}
\leqslant\dfrac{u_n}{\ln(n)}
\leqslant\dfrac{\ln(n+1)}{\ln(n)}+\dfrac{w_n}{\ln(n)}\]](/Generateur-Devoirs/Colles/Integrale/stint_c/52.png)
avec
![\[\lim_{n\to+\infty}\dfrac{\ln(n+1)}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/Integrale/stint_c/53.png)
et comme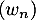 est bornée,
est bornée,
![\[\lim_{n\to+\infty}\dfrac{I}{\ln(n)}=\lim_{n\to+\infty}\dfrac{w_n}{\ln(n)}=0\]](/Generateur-Devoirs/Colles/Integrale/stint_c/55.png)
Finalement, d'après le théorème des gendarmes, on trouvé que
![\[\lim_{n\to+\infty}\dfrac{u_n}{\ln(n)}=1\]](/Generateur-Devoirs/Colles/Integrale/stint_c/56.png)
c'est-à-dire que
![\[u_n\underset{+\infty}{\sim} \ln(n)\]](/Generateur-Devoirs/Colles/Integrale/stint_c/57.png)
- La fonction
Tags:IntégraleSuites
Autres sujets au hasard:
