Sous-espaces vectoriels de suites supplémentaires
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit 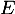 l'espace vectoriel des suites réelles,
l'espace vectoriel des suites réelles,
![\[F=\bigl\{u\in E;\ \forall n\in\mathbb N,\ u_{2n}=0\bigr\}\]](/Generateur-Devoirs/Colles/ev/exssevsuites/2.png)
![\[G=\bigl\{u\in E;\ \forall n\in\mathbb N,\ u_{2n}=u_{2n+1}\bigr\}\]](/Generateur-Devoirs/Colles/ev/exssevsuites/3.png)
Démontrer que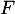 et
et 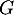 sont supplémentaires dans
sont supplémentaires dans 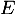
Démontrer que
Correction
En effet, si une suite appartient à l'intersection de ces deux espaces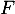 et
et 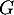 , alors elle appartient à
, alors elle appartient à 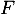 donc tous ses termes d'indice pair sont nuls, et elle appartient aussi à
donc tous ses termes d'indice pair sont nuls, et elle appartient aussi à 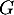 , donc tous ses termes d'indices impairs sont égaux à ceux d'indices pairs donc sont nuls aussi.
, donc tous ses termes d'indices impairs sont égaux à ceux d'indices pairs donc sont nuls aussi.
En résumé seule la suite nulle appartient à la fois à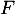 et
et 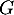 .
.
On prouve maintenant que la somme de ces deux espaces est bien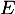 , c'est-à-dire que
, c'est-à-dire que 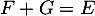 .
.
On peut procéder par analyse synthèse.
On commence par analyser la situation, et cette somme d'espace.
Soit une suite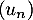 quelconque de
quelconque de 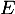 .
On cherche alors une décomposition
.
On cherche alors une décomposition 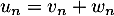 avec
avec 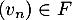 et
et 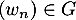 .
.
On a donc alors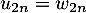 . Comme de plus
. Comme de plus 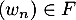 , cela définit complètement
, cela définit complètement 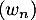 puisqu'alors
puisqu'alors 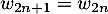 .
.
Maintenant que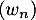 est identifiée, la suite
est identifiée, la suite 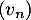 est alors simplement la différence:
est alors simplement la différence: 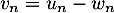 , pour laquelle il reste à vérifier qu'elle appartient bien alors à
, pour laquelle il reste à vérifier qu'elle appartient bien alors à 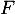 .
.
On passe à la synthèse.
Soit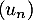 une suite quelconque de
une suite quelconque de 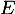 .
.
On définit la suite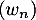 par
par 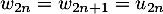 pour tout entier naturel
pour tout entier naturel 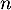 .
On a bien, par défintion,
.
On a bien, par défintion, 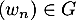 .
.
On pose ensuite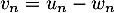 , pour tout entier naturel
, pour tout entier naturel 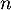 .
.
On a pour cette suite, pour tout entier naturel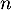 ,
,
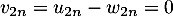 , et donc
, et donc 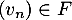 .
.
Enfin, on a bien la somme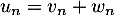 avec
avec 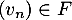 et
et 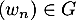 , c'est-à-dire que
, c'est-à-dire que 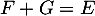 .
.
Comme on a déjà prouvé que leur intersection est réduit à la suite nulle, on sait de plus que cette somme est directe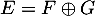 , ou en d'autres termes que ces deux sous-espace
, ou en d'autres termes que ces deux sous-espace 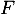 et
et 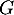 sont supplémentaires dans
sont supplémentaires dans 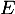 .
.
Correction
On montre tout d'abord que l'intersection de ces deux espaces est réduit à la suite nulle.En effet, si une suite appartient à l'intersection de ces deux espaces
En résumé seule la suite nulle appartient à la fois à
On prouve maintenant que la somme de ces deux espaces est bien
On peut procéder par analyse synthèse.
On commence par analyser la situation, et cette somme d'espace.
Soit une suite
On a donc alors
Maintenant que
On passe à la synthèse.
Soit
On définit la suite
On pose ensuite
On a pour cette suite, pour tout entier naturel
Enfin, on a bien la somme
Comme on a déjà prouvé que leur intersection est réduit à la suite nulle, on sait de plus que cette somme est directe
Tag:Espace vectoriel
Autres sujets au hasard:

Voir aussi: