Séries à partir d'une suite implicite
Colle de mathématiques
Sujet de colle de maths:- SériesSéries
Énoncé du sujet
Oral ESCP, BL - 2021
- Soit
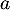 un réel positif ou nul. Pour tout
un réel positif ou nul. Pour tout 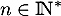 , on considère l'équation d'inconnue
, on considère l'équation d'inconnue 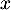 réel
réel
![\[x^n+n^ax-1=0\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2/4.png)
Montrer que cette équation admet une seule solution sur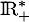 .
On la note
.
On la note  .
.
- Étudier la convergence de la suite
 .
.
- On suppose
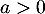 .
.
- Montrer que
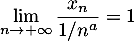
- Soit
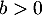 . Étudier la convergence des séries suivantes:
. Étudier la convergence des séries suivantes:
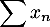 ,
,
 ,
,
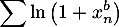 , et
, et

- Montrer que
Correction
Correction
Oral ESCP, BL - 2021- Soit
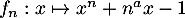 , définie et dérivable sur
, définie et dérivable sur  (et même infoiniment dérivable, c'est un polynôme), avec
(et même infoiniment dérivable, c'est un polynôme), avec
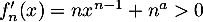 sur
sur 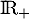 .
.
on en déduit que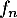 est strictement croissante sur
est strictement croissante sur 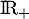 , avec
, avec
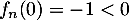 et
et 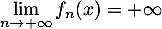 .
.
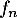 est donc une bijection de
est donc une bijection de 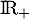 sur
sur 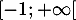 et en particulier il existe un unique réel
et en particulier il existe un unique réel 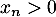 tel que
tel que 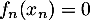 .
.
- On peut chercher un encadrement de
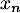 .
On a donc
.
On a donc 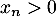 d'une part. Par ailleurs, on a
d'une part. Par ailleurs, on a 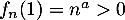 d'où
d'où 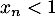 , et donc, pour tout entier
, et donc, pour tout entier 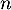 ,
,
![\[0<x_n<1\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/19.png)
La suite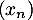 est donc bornée, mais cet encadrement est encore un peu trop large pour conclure à la convergence.
est donc bornée, mais cet encadrement est encore un peu trop large pour conclure à la convergence.
On a de plus, par définition,
![\[x_n^n+n^ax_n-1=0
\iff x_n=\dfrac{1-x_n^n}{n^a}\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/21.png)
d'où on tire, comme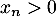 ,
,
![\[0<x_n<\dfrac1{n^a}\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/23.png)
et ainsi, d'après le théorème des gendarmes, pour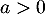 , on trouve
, on trouve
![\[\lim_{n\to+\infty}x_n=0\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/25.png)
-
- On a vus que
![\[x_n=\dfrac{1-x_n^n}{n^a}\iff \dfrac{x_n}{1/n^a}=1-x_n^n\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/26.png)
et, comme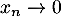 , on a aussi
, on a aussi 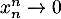 , ce qui montre bien que
, ce qui montre bien que
![\[\lim_{n\to+\infty}\dfrac{x_n}{1/n^a}=1\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/29.png)
c'est-à-dire que
![\[x_n\sim\dfrac1{n^a}\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/30.png)
- D'après le résultat précédent, on en déduit que la série
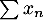 est de même nature que la série de Riemann
est de même nature que la série de Riemann 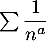 et est donc convergente si et seulement si
et est donc convergente si et seulement si 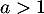 .
.
Comme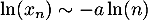 , la série
, la série 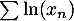 diverge grossièrement.
diverge grossièrement.
Pour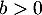 , on a
, on a 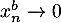 et donc
et donc 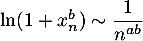 est le terme général d'une série convergente si et seulement si
est le terme général d'une série convergente si et seulement si 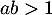 .
.
On a
![\[\left|x_n-\dfrac1{n^a}\right|=\dfrac{x_n^n}{n^a}\leqslant\dfrac1{n^a}\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/40.png)
et la série converge encore lorsque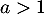 .
.
Elle converge en fait là aussi pour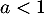 car on a majoré trop fortement le
car on a majoré trop fortement le 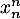 qui tend luis aussi vers 0.
qui tend luis aussi vers 0.
Plus précisément, comme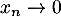 , à partir d'un certain rang on a, par exemple,
, à partir d'un certain rang on a, par exemple, 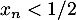 , et alors
, et alors
![\[\dfrac{x_n^n}{n^a}<\dfrac1{2^n}\]](/Generateur-Devoirs/Colles/Series/ESCP-BL-2021-4.2_c/46.png)
majoration par le terme général d'une série géométrique convergente.
Finalement, cette dernière série converge indépendamment de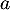 .
.
- On a vus que
Tag:Séries
Autres sujets au hasard:
