Série presque géométrique
Soit ![$x\in ]-1,1[$](/Generateur-Devoirs/Colles/Series/SG/1.png)
. Calculer 
.
. Calculer .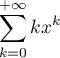
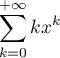Correction
On pense à la série géométrique, pour
,
![\[\sum_{k=0}^n x^k=\dfrac{1-x^{n+1}}{1-x}\]](/Generateur-Devoirs/Colles/Series/SG_c/2.png)
On dérive cette égalité (on a une somme finie, c'est-à-dire un polynôme, donc bien dérivable) :
![\[\sum_{k=1}^n kx^{k-1}=\dfrac{-(n+1)x^n(1-x)+(1-x^{n+1})}{(1-x)^2}\]](/Generateur-Devoirs/Colles/Series/SG_c/3.png)
puis, on revient à la somme qui nous intéresse:
![\[\begin{array}{ll}\dsp\sum_{k=0}^{n}kx^k&=x\dsp\sum_{k=1}^n kx^{k-1}\\[1.4em]
&\hspace{-3em}=x\dfrac{-(n+1)x^n(1-x)+(1-x^{n+1})}{(1-x)^2}\enar\]](/Generateur-Devoirs/Colles/Series/SG_c/4.png)
et il reste à prendre la limite, avec, comme
, donc
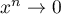et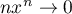 
, d'où
![\[\begin{array}{ll}\dsp\sum_{k=1}^{+\infty}kx^k&=\dsp\lim_{n\to+\infty}\dsp\sum_{k=0}^{n}kx^k\\[1.4em]
&=\dfrac{x}{(1-x)^2}\enar\]](/Generateur-Devoirs/Colles/Series/SG_c/8.png)
Cacher la correction
On pense à la série géométrique, pour
,
On dérive cette égalité (on a une somme finie, c'est-à-dire un polynôme, donc bien dérivable) :
puis, on revient à la somme qui nous intéresse:
et il reste à prendre la limite, avec, comme
, donc
et , d'où
Cacher la correction
Tag:Séries
Autres sujets au hasard:
