Réunion de deux sous-espaces vectoriels
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit  et
et 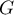 deux sous-espaces vectoriels d'un même espace vectoriel
deux sous-espaces vectoriels d'un même espace vectoriel 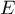 .
Montrer que
.
Montrer que
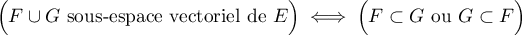 .
.
Correction
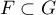 alors
alors 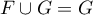 , et
si
, et
si 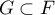 alors
alors 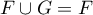 et donc,
comme
et donc,
comme 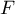 et
et 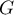 sont des sous-espaces vectoriels,
l'inclusion d'un des sous-espaces dans l'autre suffit
à ce que la réunion des deux soit aussi un sous-espace vectoriel.
sont des sous-espaces vectoriels,
l'inclusion d'un des sous-espaces dans l'autre suffit
à ce que la réunion des deux soit aussi un sous-espace vectoriel.
Montrons maintenant que c'est aussi nécessaire.
Supposons donc que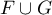 est un sous-espace vectoriel,
et que, par exemple,
est un sous-espace vectoriel,
et que, par exemple, 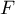 n'est pas inclus dans
n'est pas inclus dans  et
et
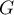 n'est pas inclus dans
n'est pas inclus dans  .
.
Il existe alors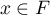 ,
, 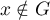 et
et 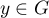 ,
, 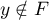 .
.
On a alors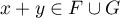 car
car 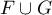 est un sous-espace vectoriel et que
est un sous-espace vectoriel et que
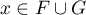 et
et  .
.
On a donc ou
ou 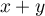 .
Mais, si
.
Mais, si 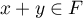 , alors
, alors  ce qui est contradictoire,
et si
ce qui est contradictoire,
et si
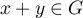 , alors
, alors 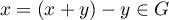 ce qui est aussi contradictoire.
ce qui est aussi contradictoire.
On a donc montré que, si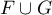 est un sous-espace vectoriel, alors
nécessairement un de ces deux sous-espaces est inclus dans l'autre.
est un sous-espace vectoriel, alors
nécessairement un de ces deux sous-espaces est inclus dans l'autre.
Correction
SiMontrons maintenant que c'est aussi nécessaire.
Supposons donc que
Il existe alors
On a alors
On a donc
On a donc montré que, si
Tag:Espace vectoriel
Autres sujets au hasard:
