Produit, logarithme et intégrales et équivalent en l'infini

Colle de mathématiques

Sujet de colle de maths:

IntégraleIntégrale

Énoncé du sujet

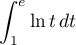
Calculer l'intégrale $\dsp\int_1^e \ln t\,dt$
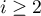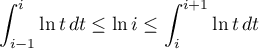Montrer que, pour tout $i\geq 2$ , $\dsp\int_{i-1}^i\ln t\,dt\leq\ln i\leq\int_i^{i+1}\ln t \,dt$ .
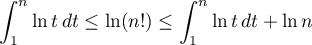Montrer que, pour tout entier $n\geq 1$ , $\dsp\int_1^n \ln t\,dt\leq \ln(n!)\leq \int_1^n\ln t \,dt+\ln n$ .
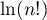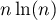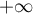En déduire que $\ln(n!)$ est équivalent à $n\ln(n)$ lorsque tend vers $+\infty$ .

Correction

On réalise une intégration par parties, en écrivant 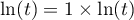$\ln(t)=1\times \ln(t)$ , d'où

$\begin{array}{ll}\dsp\int_1^e\ln(t)dt &=\Bigl[ t\ln(t)\Bigr]_1^e-\dsp\int_1^e t\tm\dfrac1tdt\\[1em] &=e\ln e-e+1 =1\enar$
Soit $t\in [i-1,i]$ . Alors, puisque la fonction logarithme est croissante, on a

$\ln(t)\leq \ln(i)$

et donc, en intègrant sur ,

$\int_{i-1}^i \ln(t)dt\leq\int_{i-1}^i\ln(i)dt=(i-(i-1))\ln(i)=\ln(i)$

La deuxième partie de l'inégalité se prouve exactement de la même façon, en remarquant que pour tout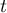 dans , on a

$\ln(i)\leq\ln(t)$
On commence par l'inégalité de gauche, en sommant membre à membre l'inégalité de gauche précédente pour allant de 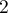jusqu'à .
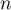Par la formule de Chasles, le membre de gauche est alors

$\int_1^2\ln(t)dt+\int_2^3\ln(t)dt+\dots+\int_{n-1}^n\ln(t)dt=\int_1^n \ln (t)dt$

Le membre du milieu vaut lui

$\sum_{i=2}^n \ln(i)=\ln\left(\prod_{i=2}^n i\right)=\ln(n!)$

On s'occupe ensuite de l'inégalité de droite. On somme membre à membre l'inégalité de droite de la question précédente, mais cette fois pour de 2 à .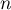
On obtient

$\ln\big((n-1)!\big)\leq \int_1^n\ln(t)dt$

Il suffit ensuite d'ajouter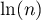 $\ln(n)$ de chaque côté de l'inégalité pour obtenir le résultat demandé.
Des deux questions précédentes, on tire

$n\ln n-n+1\leq\ln(n!)\leq n\ln n+\ln n-n+1$

soit encore

$1-\dfrac1{\ln n}+\dfrac1{n\ln n} \leq\frac{\ln(n!)}{n\ln n} \leq 1+\dfrac1n-\dfrac1{\ln n}+\dfrac1{n\ln n}$

Par le théorème des gendarmes, on trouve alors que

$\lim_{n\to+\infty}\dfrac{\ln(n!)}{n\ln (n)}=1$

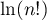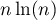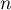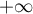Ceci signifie exactement que $\ln(n!)$ est équivalent à $n\ln(n)$ lorsque tend vers $+\infty$ .

Tag:Intégrale

Autres sujets au hasard:

Voir aussi: