Matrice d'un endomorphisme sans sous-espace stable


Colle de mathématiques

Sujet de colle de maths:
  • DiagonalisationDiagonalisation de matrice et réduction des endomorphismes

Énoncé du sujet

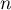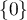Soit $u$ un endomorphisme d'un $\mathbb K$-espace vectoriel $E$ de dimension finie $n$ supérieure ou égale à 2. On suppose que $E$ et $\{0\}$ sont les seuls sous-espaces vectoriels de $E$ stables par $u$.
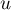  1. $u$ possède-t-il des valeurs propres ?
  2. Démontrer que pour tout 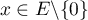$x\in E\backslash\{0\}$, la famille 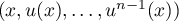$(x,u(x),\dots,u^{n-1}(x))$ est une base de $E$.
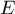  3. Donner la matrice de $u$ dans la base $(x,u(x),\dots,u^{n-1}(x))$.
    Cette matrice dépend-elle du choix de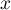 $x$ ?



Correction

Correction

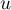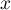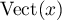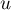  1. Si $u$ admettait un vecteur propre $x$, alors $\text{Vect}(x)$ serait un sous-espace de $E$ stable par $u$ différent de $\{0\}$ et de $E$, ce qui est impossible.
  2. Imaginons que la famille soit liée. Alors il existe $p\leq n-1$ et des scalaires $a_0,\dots,a_{p-1}$ tels que

    \[u^p(x)=a_0x+\dots+a_{p-1}u^{p-1}(x)\]

    On vérifie alors que l'espace vectoriel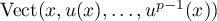 $\text{Vect}(x,u(x),\dots,u^{p-1}(x))$ est stable par $u$.
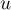  3. Soit $b_0,\dots,b_{n-1}$ des scalaires tels que
    \[u^n(x)=b_0x+\dots+b_{n-1}u^{n-1}(x)\]

    La matrice de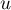 $u$ dans la base $(x,u(x),\dots,u^{n-1}(x))$ est alors
    \[\lp\begin{array}{cccc} 0&\dots&0&b_0\\ 1&\ddots&0&b_1\\ &\ddots&\vdots&\vdots\\ 0&0&1&b_{n-1}. \end{array}\rp\]

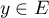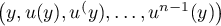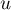    Soit maintenant $y\in E$. On a donc comme précédemment que $\left( y,u(y),u^(y),\dots,u^{n-1}(y)\rp$ est une base de $E$. Les $n-1$ premières colonnes de la matrice de $u$ dans cette base sont les mêmes que la matrice précédentes. Il reste à regarder de plus près la dernière colonne, c'est-à-dire l'expression de $u^n(y)$ dans cette base.

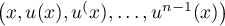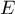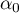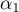    Comme $\left( x,u(x),u^(x),\dots,u^{n-1}(x)\rp$ est une base de $E$, il existe des (uniques) coefficients $\alpha_0$, $\alpha_1$, … , $\alpha_{n-1}$ tels que
    \[y=\alpha_0x+\alpha_1u(x)+\dots+\alpha_{n-1}u^{n-1}(x)\]

    et alors
    \[u^n(y)=\alpha_0u^n(x)+\alpha_1u^n(u(x))+\dots+\alpha_{n-1}u^n\left( u^{n-1}(x)\rp\]

    Or, pour tout entier $i$, on a
    \[\begin{array}{ll}u^n\left( u^i(x)\rp&=u^i\left( u^n(x)\rp \\[.5em] &=u^i\left( b_0x+b_1u(x)+\dots+b_{n-1}u^{n-1}(x)\right) \\[.5em] &=b_0u^i(x)+b_1u^{i+1}(x)+\dots+b_{n-1}u^{i+n-1}(x)\enar\]

    On a alors
    \[\begin{array}{lcl} u^n(y)&=&\alpha_0u^n(x)+\alpha_1u^n(u(x))+\dots+\alpha_{n-1}u^n\left( u^{n-1}(x)\right) \\[.5em] &=&\alpha_0\left( b_0x+b_1u(x)+\dots\right) \\ &&+\alpha_1\left( b_0u(x)+b_1u^2(x)+\dots\rp\\ &&+\alpha_2\left( b_0u^2(x)+b_1u^3(x)+\dots\rp\\ &&+\dots\\ &=&b_0\underbrace{\lp\alpha_0x+\alpha_1x+\dots\right)}_{y} +b_1\underbrace{u\lp\alpha_0x+\alpha_1x+\dots\right)}_{u(y)} +\dots \enar\]

    et on retrouve donc les mêmes coefficients pour la dernière colonne: la matrice ne dépend donc pas du choix de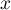 $x$.


Tag:Diagonalisation

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0