Logarithme, encadrements et convergence d'un produit
Colle de mathématiques
Sujet de colle de maths:- SommesSommes des termes d'une suite
Énoncé du sujet
- Montrer que, pour tout
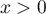 ,
,
![\[x-\dfrac{x^2}2<\ln(1+x)<x\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit/2.png)
- En déduire la limite de la suite de terme général
![\[u_n=\dsp\prod_{k=1}^n\lp1+\dfrac{k}{n^2}\rp\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit/3.png)
Correction
Correction
- Ces deux inégalités peuvent se montrer en étudiant les fonctions
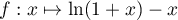 et
et 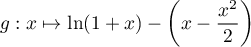 .
.
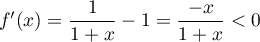 pour
pour 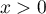 ,
donc
,
donc 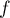 est décroissante et alors, pour tout
est décroissante et alors, pour tout 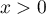 ,
,
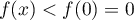 , soit
, soit
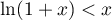 .
.
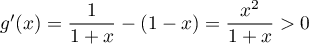 et donc
et donc
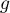 est croissante et pour tout
est croissante et pour tout 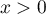 ,
,
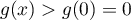 soit aussi, pour
soit aussi, pour 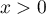 ,
,
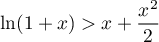 .
.
- Le produit et la question précédente incitent à utiliser le logarithme et à poser
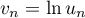 , soit
, soit
![\[v_n=\sum_{k=1}^n\ln\lp1+\dfrac{k}{n^2}\rp\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/16.png)
D'après la question précédente, on a alors,
![\[\sum_{k=1}^n\lp\dfrac{k}{n^2}-\dfrac{k^2}{2n^4}\right)
<v_n<\sum_{k=1}^n\dfrac{k}{n^2}\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/17.png)
On a de plus,
![\[\sum_{k=1}^n\dfrac{k}{n^2}=\dfrac1{n^2}\sum_{k=1}^nk=\dfrac{n(n+1)}{2n^2}
=\dfrac{n+1}{2n}\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/18.png)
et
![\[\sum_{k=1}^n\dfrac{k^2}{2n^4}
=\dfrac{1}{2n^4}\sum_{k=1}^nk^2
=\dfrac{n(n+1)(2n+1)}{12n^4}\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/19.png)
d'où l'encadrement
![\[\dfrac{n+1}{2n}-\dfrac{n(n+1)(2n+1)}{12n^4}<v_n<\dfrac{n+1}{2n}\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/20.png)
Comme
![\[\lim_{n\to+\infty}\dfrac{n+1}{2n}=\dfrac12\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/21.png)
et
![\[\dfrac{n(n+1)(2n+1)}{12n^4}\simeq\dfrac1{6n}\to0\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/22.png)
on obtient, d'après le théorème des gendarmes, que
![\[\lim_{n\to+\infty}v_n=\dfrac12\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/23.png)
et donc que
![\[\lim_{n\to+\infty}v_n=e^{1/2}=\sqrt{e}\]](/Generateur-Devoirs/Colles/Suites/exln-encadrement-Produit_c/24.png)
Tag:Sommes
Autres sujets au hasard:

Voir aussi: