Intégrale impropre avec exponentielles, et changement de variable
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
On pose 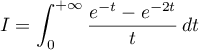 .
.
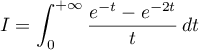 .
.
- Montrer que
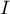 converge.
converge.
- Pour
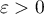 , en posant
, en posant  ,
montrer que
,
montrer que
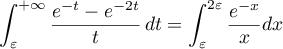 .
.
- Démontrer que, pour tout
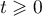 ,
,
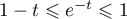 .
.
- Déduire des questions précédentes la valeur de
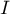 .
.
- En posant
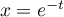 , calculer
, calculer
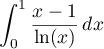 .
.
Correction
Correction
- La fonction
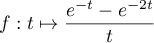 est continue sur
est continue sur ![$]0;+\infty[$](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/2.png) avec,
avec,
![\[\lim_{t\to+\infty}t^2f(t)=\lim_{t\to+\infty}t\left( e^{-t}-e^{-2t}\rp=0\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/3.png)
par croissances comparées, et donc, en ,
,
![\[f(t)=o\lp\dfrac1{t^2}\rp\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/5.png)
ce qui montre, d'après le critère de Riemann, que l'intégrale converge en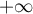 .
.
Par ailleur, en 0, on a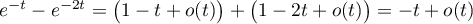 et donc
et donc
![\[\lim_{t\to0}f(t)=-1\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/8.png)
ce qui montre que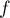 est prolongeable par continuité en 0,
et en particulier que l'intégrale converge en 0.
est prolongeable par continuité en 0,
et en particulier que l'intégrale converge en 0.
Finalement, on a montré que l'intégrale converge.
- On décompose l'intégrale, grâce à la relation de Chasles,
![\[I=\underbrace{\int_\varepsilon^{+\infty}\dfrac{e^{-t}}t\,dt}_{=I_1}
-\underbrace{\int_\varepsilon^{+\infty}\dfrac{e^{-2t}}t\,dt}_{=I_2}\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/10.png)
et on applique le changement de variable proposé: donc
donc 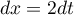 (qui est un changement de variable de class
(qui est un changement de variable de class 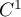 et strictement croissant)
et strictement croissant)
![\[I_2=\int_\varepsilon^{+\infty}\dfrac{e^{-2t}}t\,dt
=\int_{2\varepsilon}^{+\infty}\dfrac{e^{-x}}{\dfrac{x}2}\,\dfrac{dx}2
=\int_{2\varepsilon}^{+\infty}\dfrac{e^{-x}}{x}\,dx
\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/14.png)
puis, avec à nouveau la relation de Chasles,
![\[\begin{array}{ll}I&=I_1+I_2
=\dsp\int_\varepsilon^{+\infty}\dfrac{e^{-t}}t\,dt
-\int_{2\varepsilon}^{+\infty}\dfrac{e^{-x}}{x}\,dx\\[1.1em]
&=\dsp\int_\varepsilon^{+\infty}\dfrac{e^{-t}}t\,dt
+\int_{+\infty}^{2\varepsilon}\dfrac{e^{-x}}{x}\,dx
=\int_\varepsilon^{2\varepsilon}\dfrac{e^{-x}}{x}dx
\enar\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/15.png)
- Pour
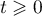 , on a directement que
, on a directement que 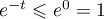 par
décroissance de la fonction
par
décroissance de la fonction 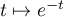 .
.
Par ailleurs, en étudiant la fonction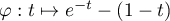 ,
on a
,
on a 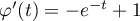 et donc
et donc
![\[\begin{tabular}{|c|ccccc|}\hline
$t$&-$\infty$ && 0 && $+\infty$ \\\hline
$\varphi'(t)$ &&$-$&0&$+$&\\\hline
&&&&&\\
$\varphi$ &&\Large{$\searrow$} &&\Large{$\nearrow$} &\\
&&&0&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/21.png)
ce qui montre que pour tout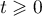 ,
,
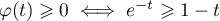 .
.
- D'après les questions précédentes, on a
![\[\int_\varepsilon^{2\varepsilon}\dfrac{1-x}{x}dx
\leqslant \int_\varepsilon^{2\varepsilon}\dfrac{e^{-x}}{x}dx
\leqslant \int_\varepsilon^{2\varepsilon}\dfrac{1}{x}dx\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/24.png)
avec, d'une part
![\[\begin{array}{ll}\dsp\int_\varepsilon^{2\varepsilon}\dfrac{1}{x}dx
&=\Bigl[\ln(x)\Bigr]_\varepsilon^{2\varepsilon}
=\ln(2\varepsilon)-\ln(\varepsilon)\\[1em]
&=\ln\lp\dfrac{2\varepsilon}{\varepsilon}\right)
=\ln(2)\enar\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/25.png)
et d'autre part,
![\[\int_\varepsilon^{2\varepsilon}\dfrac{1-x}{x}dx
=\int_\varepsilon^{2\varepsilon}\dfrac1x\,dx
-\int_\varepsilon^{2\varepsilon}1\,dx
=\ln(2)-\varepsilon\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/26.png)
L'encadrement précédent se réécrit donc,
![\[\ln(2)-\varepsilon\leqslant
\int_\varepsilon^{2\varepsilon}\dfrac{e^{-x}}{x}dx
\leqslant \ln(2)\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/27.png)
puis, par le théorème des gendarmes, à la limite ,
on obtient
,
on obtient 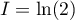 .
.
- En posant
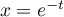 , donc
, donc 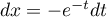 , on a
, on a
![\[\begin{array}{ll}\dsp\int_0^1\dfrac{x-1}{\ln(x)}\,dx
&=\dsp\int_{+\infty}^0\dfrac{e^{-t}-1}{-t}\lp-e^{-t}dt\rp\\[1em]
&\hspace{-4em}=\dsp\int_0^{+\infty}\dfrac{e^{-t}-e^{-2t}}t\,dt
=I=\ln(2)\enar\]](/Generateur-Devoirs/Colles/Integrale/int-impropre-exp_c/32.png)
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: