Formule des probabilités composées
Colle de mathématiques
Sujet de colle de maths:- Probabilités conditionnelles - indépendanceProbabilités conditionnelles - indépendance
Énoncé du sujet
- Énoncer et démontrer la formule des probabilités composées.
- Une urne contient initialement 7 boules noires et 3 boules blanches.
On tire successivement 3 boules : si on tire une noire, on l'enlève, si on tire une blanche, on la retire, et on ajoute une noire à la place.
Quelle est la probabilité de tirer 3 blanches à la suite ?
Correction
Correction
- Formule des probabilités composées: soit
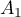 ,
, 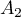 , … ,
, … ,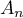 des événements tels que
des événements tels que
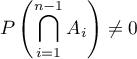 , alors
, alors
![\[P\lp\bigcap_{i=1}^nA_i\rp=P\lp A_1\rp\times P_{A_1}\lp A_2\rp\times P_{A_1\cap A_2}\lp A_3\rp
\tm\dots\tm P_{A_1\cap A_2\cap\dots\cap A_{n-1}}\left( A_n\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours1_c/5.png)
Démonstration: On démontre cette propriété par récurrence sur le nombre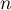 d'événements.
d'événements.
Pour , la propriété est tautologique,
et pour
, la propriété est tautologique,
et pour  ,
,
![\[P\left( A_1\cap A_2\rp=P\left( A_1\rp\times P_{A_1}\left( A_2\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours1_c/9.png)
est la définition même de la probabilité conditionnelle.
Si on suppose maintenant la propriété vraie au rang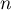 , alors au rang suivant
, alors au rang suivant 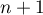 :
:
![\[\begin{array}{ll}\displaystyle P\lp\bigcap_{i=1}^{n+1} A_i\right)
&=\displaystyle P\lp\lp\bigcap_{i=1}^nA_i\rp\cap A_{n+1}\rp\\[1.4em]
&=\displaystyle P\lp\bigcap_{i=1}^nA_i\rp\times P_{A_1\cap A_2\cap\dots\cap A_n}\lp A_{n+1}\rp\enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours1_c/12.png)
en utilisant la propriété pour deux événements, et qui nous fournit le résultat en utilisant l'hypothèse de récurrence.
- On note
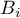 l'événement "La i-ème boule tirée est blanche".
La probabilité recherchée est
l'événement "La i-ème boule tirée est blanche".
La probabilité recherchée est 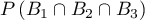 , soit avec la formule des probabilités composées:
, soit avec la formule des probabilités composées:
![\[P\left( B_1\cap B_2\cap B_3\rp=P\left( A_1\rp\times P_{B_1}\left( B_2\rp\times P_{B_1\cap B_2}\left( B_3\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours1_c/15.png)
On a d'abord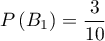 .
.
Lorsque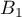 est réalisé, l'urne est constituée avant le 2ème tirage 8 boules noires et 2 blanches et donc
est réalisé, l'urne est constituée avant le 2ème tirage 8 boules noires et 2 blanches et donc
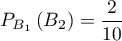 .
.
Enfin, lorsque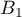 et
et 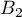 sont réalisés, l'urne contient avant le 3ème tirage 9 boules noires et 1 boule blanche et donc
sont réalisés, l'urne contient avant le 3ème tirage 9 boules noires et 1 boule blanche et donc
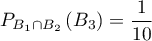 .
.
On trouve donc
![\[P\left( B_1\cap B_2\cap B_3\rp=\dfrac3{10}\tm\dfrac2{10}\tm\dfrac1{10}=\dfrac6{1000}=\dfrac3{500}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours1_c/22.png)
Tag:Probabilités conditionnelles - indépendance
Autres sujets au hasard:

Voir aussi: