File d'attente à un guichet
Dans un bureau de poste, il y a deux guichets. Chacune des personnes arrivant à la poste choisit le premier guichet avec une probabilité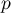 
,
ou le deuxième guichet avec une probabilité 
. Les personnes effectuent leur choix de façon indépendante. En une heure, le nombre 
de personnes arrivés à la poste suit une loi de Poisson 
.
On désigne par 
le nombre de personnes ayant choisi le premier guichet.
Correction
,
ou le deuxième guichet avec une probabilité 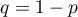. Les personnes effectuent leur choix de façon indépendante. En une heure, le nombre 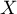de personnes arrivés à la poste suit une loi de Poisson .
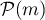On désigne par 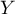le nombre de personnes ayant choisi le premier guichet.
- Exprimer la probabilité conditionnelle de
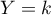sachant que 
.
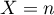- En déduire la loi conjointe du couple
.
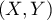- Déterminer la loi de
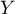. On trouvera que 
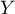suit une loi de Poisson de paramètre 
.
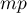Correction
Tag:Couples de variables aléatoires
Autres sujets au hasard:
