Estimation pour la loi géométrique
Colle de mathématiques
Sujet de colle de maths:- VA: inégalités & estimationVariables aléatroire: inégalités & estimation
Énoncé du sujet
Soit  un entier naturel et
un entier naturel et 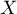 une variable aléatoire suivant la loi géométrique
une variable aléatoire suivant la loi géométrique 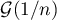 .
.
- Donner l'espérance et la variance de
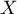 .
.
- Montrer que
 .
.
- Montrer que
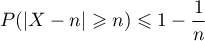 . En déduire que
. En déduire que 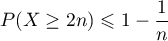 .
.
Correction
Correction
- Une variable aléatoire
 qui suit une loi géométrique de paramètre
qui suit une loi géométrique de paramètre  a pour espérance
a pour espérance 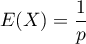 et variance
et variance 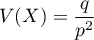 , avec
, avec 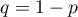 .
.
-
 étant à valeurs positives de moyenne
étant à valeurs positives de moyenne 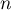 , l'inégalité de Markov donne, pour tout
, l'inégalité de Markov donne, pour tout 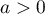 ,
,
![\[P(X\geqslant a)\leqslant \dfrac{n}a\]](/Generateur-Devoirs/Colles/VAIE/Estim-loi-geom_c/9.png)
On obtient le résultat voulu avec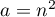 .
.
- On a
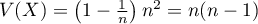 . On obtient en appliquant l'inégalité de Bienaymé-Tchebychev avec
. On obtient en appliquant l'inégalité de Bienaymé-Tchebychev avec  ,
,
![\[P(|X-n|\geqslant\varepsilon)\leqslant\dfrac{n(n-1)}{\varepsilon^2}\]](/Generateur-Devoirs/Colles/VAIE/Estim-loi-geom_c/13.png)
Pour , on obtient le résultat voulu.
, on obtient le résultat voulu.
De plus,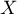 étant à valeurs dans
étant à valeurs dans  ,
les événements
,
les événements  et
et 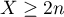 sont égaux, ce qui donne la deuxième inégalité.
sont égaux, ce qui donne la deuxième inégalité.
Tag:VA: inégalités & estimation
Autres sujets au hasard:

Voir aussi: