Estimation de pièces défectueuses produites
Colle de mathématiques
Sujet de colle de maths:- VA: inégalités & estimationVariables aléatroire: inégalités & estimation
Énoncé du sujet
Estimation de pièces défectueuses produites
[.4em] Une usine fabrique des pièces dont une proportion inconnue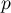 est défectueuse, et on souhaite trouver une valeur approchée de
est défectueuse, et on souhaite trouver une valeur approchée de 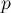 . On effectue un prélèvement de
. On effectue un prélèvement de 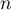 pièces. On suppose que le prélèvement se fait sur une population très grande, et donc qu'il peut s'apparenter à une suite de
pièces. On suppose que le prélèvement se fait sur une population très grande, et donc qu'il peut s'apparenter à une suite de 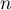 tirages indépendants avec remise. On note
tirages indépendants avec remise. On note 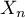 la variable aléatoire égale au nombre de pièces défectueuses et on souhaite quantifier le fait que
la variable aléatoire égale au nombre de pièces défectueuses et on souhaite quantifier le fait que 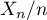 approche
approche 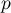 .
.
[.4em] Une usine fabrique des pièces dont une proportion inconnue
- Quelle est la loi de
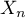 ? Sa moyenne? Sa variance?
? Sa moyenne? Sa variance?
- Démontrer que, pour tout
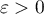 ,
,
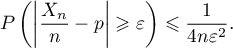
- En déduire une condition sur
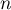 pour que
pour que 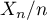 soit une valeur approchée de
soit une valeur approchée de 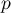 à
à 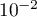 près avec une probabilité supérieure ou égale à
près avec une probabilité supérieure ou égale à 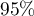 .
.
Correction
Correction
-
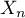 est la somme de
est la somme de 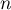 variables aléatoires de Bernoulli indépendantes de paramètre
variables aléatoires de Bernoulli indépendantes de paramètre 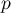 , et donc
, et donc 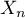 suit une loi binomiale
suit une loi binomiale 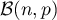 et
et
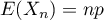 et
et 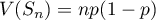 .
.
- L'inégalité de Bienaymé-Tchebychev s'écrit
![\[P(|X_n-E(X_n)|\geqslant a)\leqslant\dfrac{V(X_n)}{a^2}\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/8.png)
Or,
![\[\left|\frac{X_n}n-p\right|\geqslant\varepsilon
\iff|X_n-np|\geqslant n\varepsilon\iff |X_n-E(X_n)|\geq n\varepsilon\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/9.png)
On applique donc l'inégalité de Bienaymé-Tchebychev avec et on obtient
et on obtient
![\[P\Bigl(\left|\dfrac{X_n}n-p\right|\geqslant\varepsilon\Bigr)
\leqslant\dfrac {p(1-p)}{n\varepsilon^2}\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/11.png)
De plus, sur![$[0,1]$](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/12.png) , la fonction
, la fonction 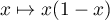 admet un maximum égal
à
admet un maximum égal
à 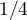 en
en 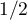 , d'où le résultat voulu.
, d'où le résultat voulu.
- On cherche
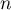 tel que
tel que
![\[P\Bigl(\left|\dfrac{X_n}n-p\right|\leqslant10^{-2}\Bigr)\geqslant0,95\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/17.png)
soit encore, en passant à l'événement contraire
![\[P\Bigl(\left|\dfrac{X_n}n-p\right|\geqslant 10^{-2}\Bigr)\leqslant 0,05\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/18.png)
Il suffit donc de choisir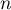 tel que
tel que
![\[\dfrac{1}{4n10^{-4}}\leqslant0,05\iff n\geqslant 5\cdot 10^4\]](/Generateur-Devoirs/Colles/VAIE/Estim-pieces-defectueuses_c/20.png)
.
Tag:VA: inégalités & estimation
Autres sujets au hasard:

Voir aussi: