Diagonalisabilité d'une matrice 2x2 symétrique réelle


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

La matrice 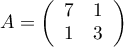$A=\lp\begin{array}{cc}7&1\\1&3\enar\rp$ est-elle diagonalisable ?


Correction

Correction

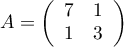La matrice $A=\lp\begin{array}{cc}7&1\\1&3\enar\rp$ est symétrique réelle, donc diagonalisable.
Si on ne connaît pas ce théorème spectral, on peut aussi (et doit savoir) le montrer.

Méthode 1: avec le polynôme caractéristique
Le polynôme caractéristique est
\[\begin{array}{ll}\chi_A(X)&=\det\left( A-XI_3\right) =\left|\begin{array}{cc}7-X&1\\1&3-X\enar\right|\\[1em] &=(7-X)(3-X)-1\\[.5em] &=X^2-10X+20\enar\]

Ce trinôme du second degré a pour discriminant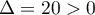 $\Delta=20>0$ et admet donc deux racines: les deuxvaleurs propres de A qui est donc diagonalisable.


avec un calcul de rang
On calcule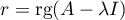 $r=\text{rg}(A-\lambda I)$, soit
\[r=\text{rg}\lp\begin{array}{cc}7-\lambda&1\\1&3-\lambda\enar\rp\]


et, $C_2\leftarrow C_2-(3-\lambda)C_1$
\[r=\text{rg}\lp\begin{array}{cc}7-\lambda&1-(3-\lambda)(7-\lambda) \\1&0\enar\rp\]

Le rang est ainsi différent de 2 lorsque
\[\begin{array}{ll} &1-(3-\lambda)(7-\lambda)=0 \\ \iff &-\lambda^2+10\lambda-20=0 \enar\]

Le discriminant de ce dernier trinôme est
\[\begin{array}{ll}\Delta&=10^2-4\tm(-1)(-20)\\ &=20>0\enar\]

A admet alors deux valeurs propres distinctes, et est donc diagonalisable.


Tags:DiagonalisationMatrices

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0