Dés pipés

Colle de mathématiques

Sujet de colle de maths:

On dispose de 100 dés dont 25 sont pipés. Pour chaque dé pipé, la probabilité d'obtenir le chiffre 6 lors d'un lancer vaut 1/2.

On tire un dé au hasard parmi les 100 dés. On lance ce dé et on obtient 6. Quelle est la probabilité que ce dé soit pipé ?
Soit 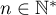$n\in\mathbb N^*$ . On tire un dé au hasard parmi 100 dé. On lance ce dé 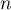fois et on obtient 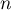fois le chiffre . Quelle est la probabilité 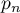pour que ce dé soit pipé.

Correction

On note les événements T: "le dé est pipé" et S: "le résultat du lancer est 6". On cherche alors .
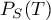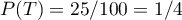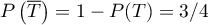On a alors donc $P\lp\overline{T}\rp=1-P(T)=3/4$ , et et bien sûr $P_{\bar T}(S)=1/6$ . La formule de Bayes donne alors

$\begin{array}{ll} P_S(T)&=\dfrac{P(T)P_T(S)}{P_T(S)P(T)+P_{\bar T}(S)P(\bar T)}\\[1.2em] &=\dfrac{\dfrac 14\tm\dfrac 12}{\dfrac 12\tm\dfrac 14+\dfrac 16\tm\dfrac34} =\dfrac12. \enar$
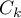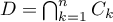On note les événements :"le k-ième lancer est un 6" et $D=\bigcap_{k=1}^n C_k$ . On cherche alors la probabilité conditionnelle .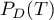
Par la formule de Bayes et grâce à l'indépendance des événements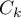 , on a

$P_T(D)=(1/2)^n$

et

$P_{\bar T}(D)=(1/6)^n$

On trouve donc:

$\begin{array}{ll} P_D(T)&=\dfrac{P(T)P_T(D)}{P_T(D)P(T)+P_{\bar T}(D)P(\bar T)}\\[1.em] &=\dfrac{\dfrac 14\tm\left(\dfrac 12\right)^n}{\left(\dfrac12\right)^n\tm\dfrac14+\left(\dfrac 16\right)^n\tm \dfrac34}\\[2.5em] &=\dfrac {1}{1+3^{-n+1}}. \enar$

En particulier,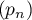 tend vers 1 lorsque 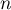tend vers l'infini, plus on observe un grand nombre de 6 consécutifs, plus la probabilité que le dé qu'on lance soit pipé est grande...

Autres sujets au hasard: