Décomposition en produits de polynômes irréductibles (bis)
Colle de mathématiques
Sujet de colle de maths:- PolynômePolynômes
Énoncé du sujet
Décomposer en produit de polynômes irréductibles de ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDecompP2/1.png) ,
,
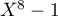 .
.
Correction
![\[\begin{array}{ll}
X^8-1
&=\left( X^4-1\rp\left( X^4+1\rp\\[.5em]
&=\left( X^2-1\rp\left( X^2+1\rp\left( X^4+1\rp\\[.5em]
&=\left( X-1\rp\left( X+1\rp\left( X^2+1\rp\left( X^4+1\rp
\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP2_c/1.png)
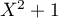 est irréductible dans
est irréductible dans ![$\R[X]$](/Generateur-Devoirs/Colles/Polynomes/exDecompP2_c/3.png) et
et 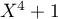 admet
admet 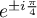 et
et 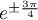 comme
racines dans
comme
racines dans 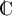 , d'où la factorisation, dans
, d'où la factorisation, dans 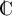 ,
,
![\[X^4+1=\left( X-e^{i\frac{3\pi}{4}}\right)
\left( X-e^{-i\frac{3\pi}{4}}\right)
\left( X-e^{i\frac\pi4}\rp\left( X-e^{-i\frac\pi4}\rp\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP2_c/9.png)
d'où la factorisation dans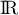 ,
,
![\[X^4+1=\left( X^2-\sqrt2X+1\rp\left( X^2+\sqrt2X+1\rp\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP2_c/11.png)
Correction
![\[\begin{array}{ll}
X^8-1
&=\left( X^4-1\rp\left( X^4+1\rp\\[.5em]
&=\left( X^2-1\rp\left( X^2+1\rp\left( X^4+1\rp\\[.5em]
&=\left( X-1\rp\left( X+1\rp\left( X^2+1\rp\left( X^4+1\rp
\enar\]](/Generateur-Devoirs/Colles/Polynomes/exDecompP2_c/1.png)
d'où la factorisation dans
Tag:Polynôme
Autres sujets au hasard:

Voir aussi: