Carré d'une loi uniforme
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit 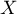 une variable aléatoire suivant une loi uniforme sur
une variable aléatoire suivant une loi uniforme sur ![$[a,b]$](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre/2.png) ,
avec
,
avec 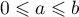 .
.
Donner la fonction de répartition, la densité et l'espérance de la variable aléatoire .
.
Donner la fonction de répartition, la densité et l'espérance de la variable aléatoire
Correction
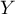 .
Si
.
Si 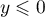 , on a
, on a 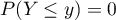 .
Si
.
Si 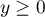 , alors
, alors
![\[\begin{array}{ll}
P(Y\leq y)&=P(-\sqrt y\leq X\leq \sqrt y)\\[.6em]
&=P(X\leq \sqrt y)\\[.6em]
&=P(X\leqslant \sqrt y)\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/5.png)
soit alors, comme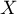 suit la loi uniforme sut
suit la loi uniforme sut ![$[0;1]$](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/7.png) ,
,
![\[P(Y\leqslant y)=\la\begin{array}{lcl}
0&\textrm{si }y\leqslant a^2\\
\dfrac{\sqrt y-a}{b-a}&\textrm{si }y\in[a^2,b^2]\\
1&\textrm{si }y\geqslant b^2.
\enar\right.\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/8.png)
La dérivée de la fonction de répartition donne la densité: On en déduit que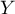 admet une densité
admet une densité 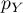 donnée par :
donnée par :
![\[f_Y(y)=\la\begin{array}{ccl}
0&\textrm{si }&y\leqslant a^2\\
\dfrac{1}{2(b-a)\sqrt y}&\textrm{si }&y\in[a^2,b^2]\\
0&\textrm{si }&y\geqslant b^2.
\enar\right.\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/11.png)
Enfin, comme , on a l'espérance
, on a l'espérance
![\[\begin{array}{ll}E(Y)=E(X^2)&=\dsp\int_a^b\frac{x^2}{b-a}dx\\[1em]
&=\dfrac{b^3-a^3}{3(b-a)}\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/13.png)
Correction
On calcule la fonction de répartion de![\[\begin{array}{ll}
P(Y\leq y)&=P(-\sqrt y\leq X\leq \sqrt y)\\[.6em]
&=P(X\leq \sqrt y)\\[.6em]
&=P(X\leqslant \sqrt y)\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/5.png)
soit alors, comme
![\[P(Y\leqslant y)=\la\begin{array}{lcl}
0&\textrm{si }y\leqslant a^2\\
\dfrac{\sqrt y-a}{b-a}&\textrm{si }y\in[a^2,b^2]\\
1&\textrm{si }y\geqslant b^2.
\enar\right.\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/8.png)
La dérivée de la fonction de répartition donne la densité: On en déduit que
![\[f_Y(y)=\la\begin{array}{ccl}
0&\textrm{si }&y\leqslant a^2\\
\dfrac{1}{2(b-a)\sqrt y}&\textrm{si }&y\in[a^2,b^2]\\
0&\textrm{si }&y\geqslant b^2.
\enar\right.\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/11.png)
Enfin, comme
![\[\begin{array}{ll}E(Y)=E(X^2)&=\dsp\int_a^b\frac{x^2}{b-a}dx\\[1em]
&=\dfrac{b^3-a^3}{3(b-a)}\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-carre_c/13.png)
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: