Caractérisation d'une similitude

Colle de mathématiques

Sujet de colle de maths:

Espaces euclidiensEspaces euclidiens, produit scalaire

Énoncé du sujet

Soit $E=\R^n$ muni du produit scalaire canonique, $f\in\mathcal L(E)$ et $\lambda>0$ . On dit que

est une similitude de rapport $\lambda$ si pour tout $x\in E$ , $\|f(x)\|=\lambda \|x\|$ .

Soit $u,v\in E$ tels que $u+v\perp u-v$ . Démontrer que $\|u\|=\|v\|$ .
Démontrer que est une similitude de rapport $\lambda$ si et seulement si, pour tous $x,y\in E$ , $\langle f(x),f(y)\rangle =\lambda^2 \langle x,y\rangle.$
On souhaite prouver que est une similitude si et seulement est non-nulle et conserve l'orthogonalité: pour tout couple , si , alors .
1. Prouver le sens direct.
2. Soit $(e_1,\dots,e_n)$ une base orthonormale de . Démontrer que, pour tout couple , $\|f(e_i)\|=\|f(e_j)\|$ .
3. Démontrer le sens réciproque.

Correction

On a, en utilisant la bilinéarité et la symétrie du produit scalaire,

$\begin{array}{ll}\langle u+v,u-v\rangle&=\|u\|^2- \langle u,v\rangle +\langle v,u\rangle -\|v\|^2\\ &=\|u\|^2-\|v\|^2\enar$

et ainsi,

$\langle u+v,u-v\rangle=0 \iff \|u\|^2=\|v\|^2$
Bien sûr, le sens réciproque est trivial puisqu'il suffit de choisir .
Réciproquement, supposons que pour tout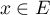 $x\in E$ , on a 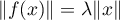$\|f(x)\|=\lambda\|x\|$ . Alors, d'une part

$\begin{array}{ll} \|f(x+y)\|^2&=\|\lambda(x+y)\|^2\\[.4em] &=\lambda^2\|x+y\|^2\\[.4em] &=\lambda^2\langle x+y,x+y\rangle\\[.4em] &=\lambda^2\Bigl( \|x\|^2+2\langle x,y\rangle +\|y\|^2\Bigr) \enar$

et d'autre part

$\begin{array}{ll}\|f(x+y)\|^2&=\langle f(x+y),f(x+y)\rangle\\[.4em] &=\|f(x)\|^2+2\langle f(x),f(y)\rangle+\|f(y)\|^2\\[.5em] &=\lambda^2\|x\|^2+2\langle f(x),f(y)\rangle+\lambda^2\|y\|^2\end{array}$

En égalant ces deux dernières relations, on obtient donc

$\langle f(x),f(y)\rangle=\lambda^2 \langle x,y\rangle$
1. C'est une conséquence directe de la question précédente.
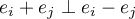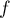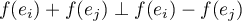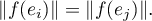
2. On sait que $e_i+e_j\perp e_i-e_j$ . Puisque préserve l'orthogonalité, $f(e_i)+f(e_j)\perp f(e_i)-f(e_j)$ . Et d'après la première question, $\|f(e_i)\|=\|f(e_j)\|.$
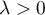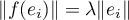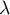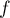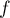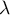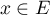3. Soit $\lambda>0$ tel que $\|f(e_i)\|=\lambda \|e_i\|$ ( $\lambda$ ne dépend pas de d'après la question précédente, et est strictement positif sinon serait nulle). On va démontrer que est une similitude de rapport $\lambda$ . Soit $x\in E$ qui s'écrit
  
  $x=\sum_{i=1}^n x_i e_i$
  
  Alors
  
  $f(x)=\sum_{i=1}^n x_if(e_i)$
  
  La famille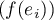 étant orthogonale, on a
  
  $\begin{array}{lcl} \|f(x)\|^2&=&\dsp\sum_{i=1}^n |x_i|^2\|f(e_i)\|^2\\ &=&\lambda^2\dsp\sum_{i=1}^n |x_i|^2\\[1.2em] &=&\lambda^2\|x\|^2. \enar$
  
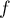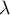  est bien une similitude de rapport $\lambda$ .

Tag:Espaces euclidiens

Autres sujets au hasard:

Voir aussi: