Accroissements finis pour un trinôme du second degré - Interprétation géométrique
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Appliquer la formule des accroissements finis
à la fonction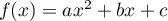 
entre 
et 
.
Que remarque-t'on ? Géométriquement ?
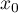entre et .
Que remarque-t'on ? Géométriquement ?
Correction
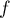est continue et dérivable sur 
(c'est un polynôme du second degré),
et la formule des accroissements finis
sur 
nous donne
l'existence de ![$\theta\in\left] x_0;x_0+h\right[$](/Generateur-Devoirs/Colles/Calcul/exAF1_c/4.png)
tel que
![\[f\left( x_0+h\rp-f\left( x_0\rp=hf'\left(\theta\rp\]](/Generateur-Devoirs/Colles/Calcul/exAF1_c/5.png)
avec,
![\[\begin{array}{ll}
f\left( x_0+h\rp-f\left( x_0\rp
&=a\left( x_0+h\rp^2+b\left( x_0+h\rp+c
-\Bigl( ax_0^2+bx_0+c\Bigr) \\[.7em]
&=2ax_0h+ah^2+bh \\[.7em]
&=h\left( 2ax_0+ah+b\right)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exAF1_c/6.png)
et
![\[f'\lp\theta\rp=2a\theta+b\]](/Generateur-Devoirs/Colles/Calcul/exAF1_c/7.png)
On a donc,
![\[f\left( x_0+h\rp-f\left( x_0\rp=hf'\left(\theta\rp
\iff h\left( 2ax_0+ah+b\rp=h\Bigl( 2a\theta+b\Bigr)\]](/Generateur-Devoirs/Colles/Calcul/exAF1_c/8.png)
et alors, pour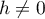
, on peut déterminer le réel 
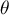de la formule des accroissements finis:
![\[\theta=x_0+\dfrac{h}2\]](/Generateur-Devoirs/Colles/Calcul/exAF1_c/11.png)
Géométriquement, cela signifie que, pour une parabole (la courbe de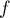
, qui est un trinôme du second degré),
la tangente au point d'abscisse 
,
milieu de 
et 
, est parallèle
à la courbe reliant les points de la parabole
et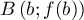 
.
![\[\psset{xunit=1.6cm,yunit=1cm,arrowsize=7pt}
\begin{pspicture}(-1,-1)(3,6)
\newcommand{\f}[1]{#1 2 exp #1 sub 1 add}
\newcommand{\fp}[1]{2 #1 mul 1 sub}
\psline{->}(-1,0)(3,0)
\psline{->}(0,-1)(0,6)
\psplot[linewidth=1.6pt]{-1}{2.6}{\f{x}}
\newcommand{\xa}{0.4}\newcommand{\xb}{2}
\newcommand{\xc}{1.2}
\psline[linestyle=dashed](\xa,0)(! \xa\space\f{\xa})
\psline[linestyle=dashed](\xb,0)(! \xb\space\f{\xb})
\rput(!\xa\space -.3){$a$}
\rput(!\xb\space -.3){$b$}
\rput(!\xc\space -.3){$\frac{a+b}{2}$}
\psline(!\xa\space\f{\xa})(!\xb\space\f{\xb})
\psline[linestyle=dashed](\xc,0)(! \xc\space\f{\xc})
\psplot{-0.3}{3}{\fp{\xc} x 1.2 sub mul \f{\xc} add}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exAF1_c/18.png)
Correction
est continue et dérivable sur
(c'est un polynôme du second degré),
et la formule des accroissements finis
sur nous donne
l'existence de tel que
avec,
et
On a donc,
et alors, pour
, on peut déterminer le réel
de la formule des accroissements finis:
Géométriquement, cela signifie que, pour une parabole (la courbe de
, qui est un trinôme du second degré),
la tangente au point d'abscisse ,
milieu de et , est parallèle
à la courbe reliant les points de la parabole
et .
Tag:Rolle - AF
Autres sujets au hasard:
Voir aussi: