Equations et intersections de deux cercles et tangentes
Exercice corrigé - Spécialité maths, première générale
Le plan est muni d'un repère orthonormé.
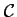 est le cercle d'équation:
est le cercle d'équation:
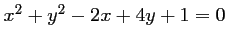 .
.
![]() est le point de coordonnées
est le point de coordonnées ![]() .
.
- a)
- Déterminer les coordonnées du centre
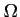 du cercle
du cercle
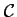 et son rayon.
et son rayon.
- b)
- Tracer le cercle
 et placer le point
et placer le point 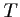 sur la
figure.
sur la
figure.
- On mène, à partir du point
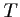 , les deux tangentes au cercle
, les deux tangentes au cercle
 et on note
et on note  et
et 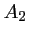 les points de contact de ces
tangentes avec
les points de contact de ces
tangentes avec
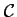 .
.
- a)
- Démontrer que
 et
et 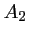 appartiennent au cercle
appartiennent au cercle
 de diamètre
de diamètre
![$ [\Omega T]$](/Generateur-Devoirs/1S/Chap6/ex4_img9.png) .
.
- b)
- Déterminer une équation du cercle
 .
.
- c)
- Calculer les coordonnées des points
 et
et 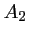 .
.
Correction
Cacher la correction
- a)
-
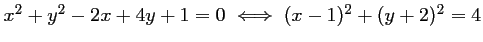 .
.
Le cercle
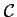 a donc pour centre
a donc pour centre
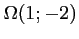 et rayon
et rayon 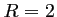 .
.
- b)
-
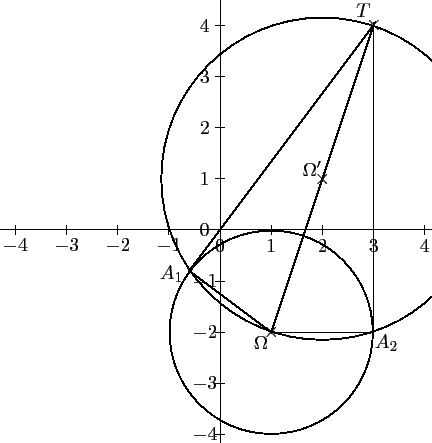
- a)
- La droite
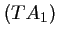 est tangente au cercle
est tangente au cercle
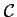 , et on
a donc,
, et on
a donc,
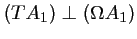 .
.
Ainsi, le triangle
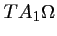 est rectangle en
est rectangle en 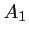 , et
, et 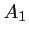 est donc sur le cercle de diamètre l'hypoténuse
est donc sur le cercle de diamètre l'hypoténuse
![$ [\Omega T]$](/Generateur-Devoirs/1S/Chap6/ex4_c_img10.png) .
.
De la même façon,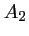 est sur le cercle de diamètre
est sur le cercle de diamètre
![$ [\Omega T]$](/Generateur-Devoirs/1S/Chap6/ex4_c_img10.png) .
.
- b)
- Le cercle
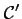 , de diamètre
, de diamètre
![$ [\Omega T]$](/Generateur-Devoirs/1S/Chap6/ex4_c_img10.png) a pour
centre le milieu de
a pour
centre le milieu de
![$ [\Omega T]$](/Generateur-Devoirs/1S/Chap6/ex4_c_img10.png) ,
soit
,
soit
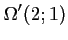 .
.
Le rayon de ce cercle est
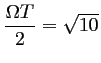 .
.
Ainsi, une équation de
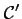 est
est
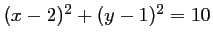 ou encore,
ou encore,
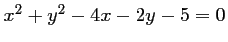 .
.
- c)
- On cherche
![$ M(x;y)\in \mathcal{C}\cup\mathcal{C}'
\iff
\left\{\begin{array}{ll}
x^2+y^2-2x+4y+1=0\\ [0.3cm]
x^2+y^2-4x-2y-5=0
\end{array}\right.
$](/Generateur-Devoirs/1S/Chap6/ex4_c_img17.png)
En soustrayant ces deux équations, on obtient:
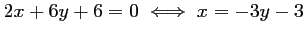 , puis, en substituant dans une des
deux équations de cercle (dans celle de
, puis, en substituant dans une des
deux équations de cercle (dans celle de
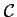 par exemple
ici):
par exemple
ici):
![\begin{displaymath}\begin{array}{ll}
\left\{\begin{array}{ll}
x^2+y^2-2x+4y+1=...
...
10y^2+28y+16=0 \\ [0.2cm]
&\iff
5y^2+14y+8=0
\end{array} \end{displaymath}](/Generateur-Devoirs/1S/Chap6/ex4_c_img19.png) .
.
Cette équation du second degré a pour discriminant
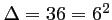 , et admet donc deux racines:
, et admet donc deux racines:
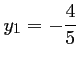 et
et 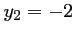 .
.
Les abscisses correspondantes sont:
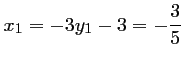 et
et
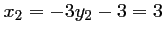 .
.
Les points d'intersections sont donc
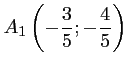 et
et 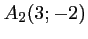 .
.
Cacher la correction
Tag:Produit scalaire
Voir aussi:
