Devoir de maths corrigé, Annale Bac, spé maths - 19 juin 2024
Terminale générale, spécialité mathématiques
Baccalauréat 12 mai 2022. Sujet posé en spécialité mathématiques, filière générale. Correction détaillée du sujet.
Exercice 1: Vrai ou faux, limites de suites et fonctions, et une équation différentielle
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
Bac 2024 (4 points) Affirmation 1 : Vrai. On a, par croissances comparées,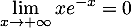 et donc
et donc 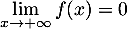 , ce qui signifie exactement que l'axe des abscisses est une asymptote horizontale à la courbe
, ce qui signifie exactement que l'axe des abscisses est une asymptote horizontale à la courbe 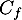 en
en 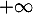 .
.
Affirmation 2 : Vrai. On dérive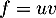 avrc
avrc 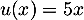 donc
donc 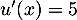 et
et 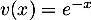 donc
donc 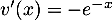 .
.
Ainsi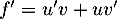 soit
soit 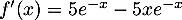 et alors on trouve que
et alors on trouve que
![\[\begin{array}{ll}f'(x)+f(x)&=5e^{-x}-5xe^{-x}+5xe^{-x}\\&=5r^{-x}\enar\]](/Generateur-Devoirs/TS/ChapQCM/VraiFaux2024_c/12.png)
ce qui montre que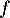 est bien une solution sur
est bien une solution sur 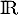 de l'équation différentielle
de l'équation différentielle 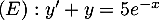 .
.
Affirmation 3 : Faux. On ne peut pas conclure ici que la suite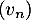 converge. Pour appliquer le théorème des gendarmes il faudrait que les limites des suites encadrantes
converge. Pour appliquer le théorème des gendarmes il faudrait que les limites des suites encadrantes 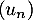 et
et  soient égales.
soient égales.
Par exemple la suite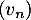 définie par
définie par 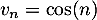 est encadrée par
est encadrée par
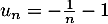 et
et 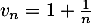 qui convergent respectivement vers
qui convergent respectivement vers 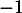 et
et 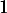 .
.
Mais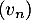 ne converge par.
ne converge par.
Affirmation 4 : Vrai.
Comme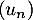 est croissante, on a pour tout entier
est croissante, on a pour tout entier 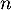 ,
,
![\[u_0\leqslant u_1\leqslant \dots \leqslant u_n\leqslant v_n\]](/Generateur-Devoirs/TS/ChapQCM/VraiFaux2024_c/28.png)
et de même, comme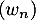 est décroissante,
est décroissante,
![\[w_0\geqslant w_1\geqslant \dots \geqslant w_n\geqslant v_n\]](/Generateur-Devoirs/TS/ChapQCM/VraiFaux2024_c/30.png)
et ainsi, en particulier,
![\[u_0 \leqslant v_n \leqslant w_0\]](/Generateur-Devoirs/TS/ChapQCM/VraiFaux2024_c/31.png)
Cacher la correction
- On considère la fonction
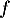 définie sur
définie sur 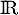 par :
par : 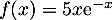 .
.
On note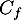 la courbe représentative de
la courbe représentative de 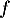 dans un repère orthonormé.
dans un repère orthonormé.
Affirmation 1 :
L'axe des abscisses est une asymptote horizontale à la courbe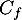 .
.
Affirmation 2 :
La fonction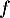 est solution sur
est solution sur 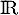 de l'équation différentielle
de l'équation différentielle 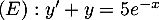 .
.
- On considère les suites
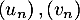 et
et 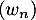 , telles que, pour tout entier naturel
, telles que, pour tout entier naturel 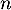 :
: 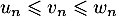 .
.
De plus, la suite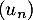 converge vers -1 et la suite
converge vers -1 et la suite 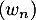 converge vers 1.
converge vers 1.
Affirmation 3 :
La suite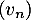 converge vers un nombre réel
converge vers un nombre réel 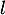 appartenant à l'intervalle
appartenant à l'intervalle ![$[-1 ; 1]$](/Generateur-Devoirs/TS/ChapQCM/VraiFaux2024/18.png) .
.
On suppose de plus que la suite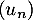 est croissante et que la suite
est croissante et que la suite 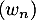 est décroissante.
est décroissante.
Affirmation 4 :
Pour tout entier naturel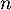 , on a alors :
, on a alors : 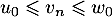 .
.
Correction exercice 1
Bac 2024 (4 points) Affirmation 1 : Vrai. On a, par croissances comparées,
Affirmation 2 : Vrai. On dérive
Ainsi
ce qui montre que
Affirmation 3 : Faux. On ne peut pas conclure ici que la suite
Par exemple la suite
Mais
Affirmation 4 : Vrai.
Comme
et de même, comme
et ainsi, en particulier,
Cacher la correction
Exercice 2: Arbre, loi binomiale, somme de variables et Bienaymé-Tchebychev
Une agence de marketing a étudié la satisfaction des clients concernant le service clientèle à l'occasion de l'achat d'un téléviseur. Ces achats ont été réalisés soit sur internet, soit dans une chaîne de magasins d'électroménager, soit dans une enseigne de grandes surfaces.
Les achats sur internet représentent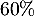 des ventes, les achats en magasin d'électroménager
des ventes, les achats en magasin d'électroménager 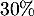 des ventes et ceux en grandes surfaces
des ventes et ceux en grandes surfaces 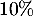 des ventes.
des ventes.
Une enquête montre que la proportion des clients satisfaits du service clientèle est de :
On choisit au hasard un client ayant acheté le modèle de téléviseur concerné.
On définit les événements suivants :
Si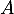 est un événement quelconque, on notera
est un événement quelconque, on notera 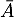 son événement contraire et
son événement contraire et 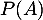 sa probabilité.
sa probabilité.
Bac 2024, 5 points
Cacher la correction
Les achats sur internet représentent
Une enquête montre que la proportion des clients satisfaits du service clientèle est de :
-
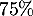 pour les clients sur internet;
pour les clients sur internet;
-
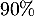 pour les clients en magasin d'électroménager ;
pour les clients en magasin d'électroménager ;
-
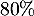 pour les clients en grande surface.
pour les clients en grande surface.
On choisit au hasard un client ayant acheté le modèle de téléviseur concerné.
On définit les événements suivants :
-
 : « le client a effectué son achat sur internet» ;
: « le client a effectué son achat sur internet» ;
-
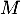 : « le client a effectué son achat en magasin d'électroménager»;
: « le client a effectué son achat en magasin d'électroménager»;
-
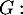 : « le client a effectué son achat en grande surface»;
: « le client a effectué son achat en grande surface»;
-
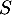 : « le client est satisfait du service clientèle».
: « le client est satisfait du service clientèle».
Si
- Reproduire et compléter l'arbre suivant.
![\[\psset{xunit=1cm,yunit=1.5cm}
\begin{pspicture}(0,-2)(5,2)
\psline(0,0)(1.5,1.5)\rput(0.6,1){\small \dots}
\rput(1.75,1.5){$I$}
\psline(3.5,2.)(2,1.5)(3.5,1)
\rput(2.7,2){\small \dots}\rput(3.7,2){$S$}
\rput(2.7,1){\small \dots}\rput(3.7,1){$\overline{S}$}
%
\psline(0,0)(1.5,0)\rput(1,0.2){\small \dots}
\rput(1.75,0){$M$}
\psline(3.5,0.5)(2,0)(3.5,-.5)
\rput(2.7,.5){\small \dots}\rput(3.7,.5){$S$}
\rput(2.7,-.5){\small \dots}\rput(3.7,-.5){$\overline{S}$}
%
\psline(0,0)(1.5,-1.5)\rput(0.6,-1.){\small \dots}
\rput(1.75,-1.5){$G$}
\psline(3.5,-2.)(2,-1.5)(3.5,-1)
\rput(2.7,-2){\small \dots}\rput(3.7,-2){$\overline{S}$}
\rput(2.7,-1){\small \dots}\rput(3.7,-1){$S$}
%
\end{pspicture}
\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024/14.png)
- Calculer la probabilité que le client ait réalisé son achat sur internet et soit satisfait du service clientèle.
- Démontrer que
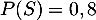 .
.
- Un client est satisfait du service clientèle. Quelle est la probabilité qu'il ait effectué son achat sur internet? On donnera un résultat arrondi à
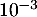 près.
près.
- Pour réaliser l'étude, l'agence doit contacter chaque jour 30 clients parmi les acheteurs du téléviseur. On suppose que le nombre de clients est suffisamment important pour assimiler le choix des 30 clients à un tirage avec remise. On note
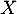 la variable aléatoire qui, à chaque échantillon de 30 clients, associe le nombre de clients satisfaits du service clientèle.
la variable aléatoire qui, à chaque échantillon de 30 clients, associe le nombre de clients satisfaits du service clientèle.
- Justifier que
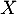 suit une loi binomiale dont on précisera les paramètres.
suit une loi binomiale dont on précisera les paramètres.
- Déterminer la probabilité, arrondie à
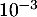 près, qu'au moins 25 clients soient satisfaits dans un échantillon de 30 clients contactés sur une même journée.
près, qu'au moins 25 clients soient satisfaits dans un échantillon de 30 clients contactés sur une même journée.
- Justifier que
- En résolvant une inéquation, déterminer la taille minimale de l'échantillon de clients à contacter pour que la probabilité qu'au moins l'un d'entre eux ne soit pas satisfait soit supérieure à 0,99.
- Dans les deux questions a. et b. qui suivent, on ne s'intéresse qu'aux seuls achats sur internet.
Lorsqu'une commande de téléviseur est passée par un client, on considère que le temps de livraison du téléviseur est modélisé par une variable aléatoire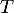 égale à la somme de deux variables aléatoires
égale à la somme de deux variables aléatoires 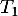 et
et 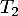 .
.
La variable aléatoire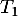 modélise le nombre entier de jours pour l'acheminement du téléviseur depuis un entrepôt de stockage vers une plateforme de distribution. La variable aléatoire
modélise le nombre entier de jours pour l'acheminement du téléviseur depuis un entrepôt de stockage vers une plateforme de distribution. La variable aléatoire 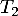 modélise le nombre entier de jours pour l'acheminement du téléviseur depuis cette plateforme jusqu'au domicile du client.
modélise le nombre entier de jours pour l'acheminement du téléviseur depuis cette plateforme jusqu'au domicile du client.
On admet que les variables aléatoires et
et 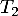 sont indépendantes, et on donne :
sont indépendantes, et on donne :
- L'espérance
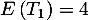 et la variance
et la variance 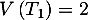 ;
;
- L'espérance
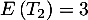 et la variance
et la variance 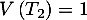 .
.
- Déterminer l'espérance
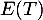 et la variance
et la variance 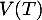 de la variable aléatoire
de la variable aléatoire 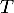 .
.
- Un client passe une commande de téléviseur sur internet. Justifier que la probabilité qu'il reçoive son téléviseur entre 5 et 9 jours après sa commande est supérieure ou égale à
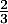 .
.
- L'espérance
Correction exercice 2
Bac 2024, 5 points
-
![\[\psset{xunit=1cm,yunit=1.5cm}
\begin{pspicture}(0,-2)(5,2)
\psline(0,0)(1.5,1.5)\rput(0.6,1){\small 60\%}
\rput(1.75,1.5){$I$}
\psline(3.5,2.)(2,1.5)(3.5,1)
\rput(2.7,2){\small 75\%}\rput(3.7,2){$S$}
\rput(2.7,1){\small 25\%}\rput(3.7,1){$\overline{S}$}
%
\psline(0,0)(1.5,0)\rput(1,0.2){\small 30\%}
\rput(1.75,0){$M$}
\psline(3.5,0.5)(2,0)(3.5,-.5)
\rput(2.7,.5){\small 90\%}\rput(3.7,.5){$S$}
\rput(2.7,-.5){\small 10\%}\rput(3.7,-.5){$\overline{S}$}
%
\psline(0,0)(1.5,-1.5)\rput(0.6,-1.){\small 10\%}
\rput(1.75,-1.5){$G$}
\psline(3.5,-2.)(2,-1.5)(3.5,-1)
\rput(2.7,-2){\small 20\%}\rput(3.7,-2){$\overline{S}$}
\rput(2.7,-1){\small 80\%}\rput(3.7,-1){$S$}
%
\end{pspicture}
\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/1.png)
- La probabilité que le client ait réalisé son achat sur internet et soit satisfait du service clientèle est la probabilité de l'intersection
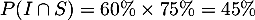
- D'après la formule des probabilités totales, on a
![\[\begin{array}{ll}P(S)&=P(I\cap S) + P(M\cap S) + P(G\cap S)\\[.6em]
&=60\%\tm75\% + 30\%\tm90\% + 10\%\tm80\%\\[.6em]
&=80\%\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/3.png)
- Sachant que le client est satisfait du service clientèle, la probabilité qu'il ait effectué son achat sur internet est
![\[P_S(I) = \dfrac{P(I\cap S)}{P(I)}=\dfrac{45\%}{80\%}\simeq56,2\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/4.png)
-
- On répète
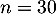 fois l'expérience aléatoire: « contacter un client au hasard», de manière identique et indépendante (car le choix est assimilé à un tirage avec remise), et dont le succès est « le client est satisfait» de probabilité
fois l'expérience aléatoire: « contacter un client au hasard», de manière identique et indépendante (car le choix est assimilé à un tirage avec remise), et dont le succès est « le client est satisfait» de probabilité 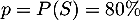 .
.
Ainsi, la variable aléatoire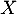 égale au nombre de succès, c'est-à-dire au nombre de clients satisfaits dans l'échantillon, suit la loi binomiale de paramètre
égale au nombre de succès, c'est-à-dire au nombre de clients satisfaits dans l'échantillon, suit la loi binomiale de paramètre 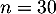 et
et 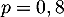 .
.
- Avec la calculatrice, on trouve que
![\[P(X\geqslant25) = 1 - P(X\leqslant 24) \simeq 0,427 = 42,7\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/10.png)
- On répète
- On cherche la taille minimale
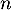 de l'échantillon pour que
de l'échantillon pour que 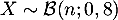 et
et
![\[P(X\leqslant n-1) = 1-P(X=n)\geqslant0,99\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/13.png)
soit
![\[\begin{array}{ll}&1-0,8^n\geqslant0,99\\
\iff&0,8^n\leqslant 1-0,99=0,01\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/14.png)
et donc, en appliquant le logarithme qui est croissant, on obtient
![\[\ln\left( 0,8^n\rp=n\ln(0,8)\leqslant\ln(0,01)\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/15.png)
et alors, en divisant par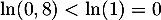 , on trouve donc
, on trouve donc
![\[n\geqslant\dfrac{\ln(0,01)}{\ln(0,8)}\simeq 20,6\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/17.png)
Il faut dnc contacter au moins 21 clients.
-
- Par linéarité de l'espérance on
![\[E(T)=E(T_1+T_2)=E(T_1)+E(T_2)=7\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/18.png)
et, comme les variables sont indépendantes, on a
![\[V(T)=V(T_1+T_2)=V(T_1)+V(T_2)=3\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/19.png)
- On cherche ici
![\[\begin{array}{ll}P\left( 5\leqslant T\leqslant9\right)
&=P\left( -2\leqslant T-7\leqslant2\rp\\[.6em]
&=P\lp|T-7|\leqslant2\rp\\[.6em]
&=1-P\lp|T-7|>2\rp\end{array}
\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/20.png)
Or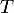 est le nombre de jours entiers, et donc
est le nombre de jours entiers, et donc
![\[P\lp|T-7|>2\rp=P\lp|T-7|\geqslant3\rp\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/22.png)
On applique alors l'inégalité de Bienaymé-Tchebychev
![\[P\left( |T-E(T)|\geqslant a\right) \leqslant \dfrac{V(T)}{a^2}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/23.png)
soit ici, avec ,
,
![\[P\left( |T-7|\geqslant 3\right) \leqslant \dfrac39=\dfrac13\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/25.png)
et alors
![\[P\lp|T-7|\geqslant3\right)
=1-P\left( 5\leqslant T\leqslant9\rp\leqslant\dfrac13\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/26.png)
d'où
![\[P\left( 5\leqslant T\leqslant9\rp\geqslant1-\dfrac13=\dfrac23\]](/Generateur-Devoirs/TS/ChapProbabilites/ex19062024_c/27.png)
- Par linéarité de l'espérance on
Cacher la correction
Exercice 3: Un peu toute la géométrie dans l'espace avec un tétraèdre
L'espace est muni d'un repère orthonormé 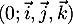 .
.
On considère les points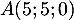 ,
, 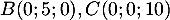 et
et 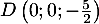 .
.
(2,2)(3,1)(6,2)
\pscircle[fillstyle=solid,fillcolor=black](0,10){.08}
\pscircle[fillstyle=solid,fillcolor=black](2,2){.08}
\pscircle[fillstyle=solid,fillcolor=black](3,1){.08}
\pscircle[fillstyle=solid,fillcolor=black](6,2){.08}
\pscircle[fillstyle=solid,fillcolor=black](0,-2.5){.08}
\psline(0,10)(2,2)(3,1)(6,2)(0,10)(3,1)
\psline[linestyle=dotted](2,2)(6,2)
\psline[linestyle=dotted](2,2)(4.3,4.3)
\psline(4.3,4.3)(5.5,5.5)
%
\rput[r](-.1,-.7){\small$O$}
\rput[r](-.3,10.2){$C$}
\rput[r](-.3,-2.6){$D$}
\rput(1.3,2.1){$B$}
\rput(3,.4){$H$}
\rput(6.4,1.8){$A$}
%
\psline{->}(0,0)(.8,.8)
\psline{->}(0,0)(0,1)
\psline{->}(0,0)(1,0)
\rput(.5,-.4){$\vec{j}$}
\rput(-.4,.8){$\vec{k}$}
\rput(.7,1.2){$\vec{i}$}
\end{pspicture}
\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024/5.png)
Bac 2024, 5 points
Cacher la correction
On considère les points
(2,2)(3,1)(6,2)
\pscircle[fillstyle=solid,fillcolor=black](0,10){.08}
\pscircle[fillstyle=solid,fillcolor=black](2,2){.08}
\pscircle[fillstyle=solid,fillcolor=black](3,1){.08}
\pscircle[fillstyle=solid,fillcolor=black](6,2){.08}
\pscircle[fillstyle=solid,fillcolor=black](0,-2.5){.08}
\psline(0,10)(2,2)(3,1)(6,2)(0,10)(3,1)
\psline[linestyle=dotted](2,2)(6,2)
\psline[linestyle=dotted](2,2)(4.3,4.3)
\psline(4.3,4.3)(5.5,5.5)
%
\rput[r](-.1,-.7){\small$O$}
\rput[r](-.3,10.2){$C$}
\rput[r](-.3,-2.6){$D$}
\rput(1.3,2.1){$B$}
\rput(3,.4){$H$}
\rput(6.4,1.8){$A$}
%
\psline{->}(0,0)(.8,.8)
\psline{->}(0,0)(0,1)
\psline{->}(0,0)(1,0)
\rput(.5,-.4){$\vec{j}$}
\rput(-.4,.8){$\vec{k}$}
\rput(.7,1.2){$\vec{i}$}
\end{pspicture}
\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024/5.png)
-
- Montrer que
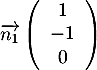 est un vecteur normal au plan (CAD).
est un vecteur normal au plan (CAD).
- En déduire que le plan (CAD) a pour équation cartésienne :
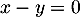 .
.
- Montrer que
- On considère la droite
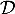 de représentation paramétrique
de représentation paramétrique
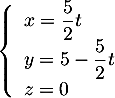 où
où 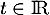 .
.
- On admet que la droite
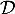 et le plan (CAD) sont sécants en un point
et le plan (CAD) sont sécants en un point 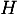 . Justifier que les coordonnées de
. Justifier que les coordonnées de 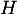 sont
sont 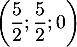 .
.
- Démontrer que le point
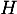 est le projeté orthogonal de
est le projeté orthogonal de 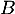 sur le plan (CAD).
sur le plan (CAD).
- On admet que la droite
-
- Démontrer que le triangle
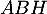 est rectangle en
est rectangle en 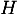 .
.
- En déduire que l'aire du triangle
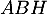 est égale à
est égale à 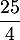 .
.
- Démontrer que le triangle
-
- Démontrer que (CO) est la hauteur du tétraèdre
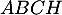 issue de
issue de 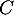 .
.
- En déduire le volume du tétraèdre
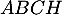 .
.
On rappelle que le volume d'un tétraèdre est donné par: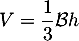 où
où 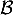 est l'aire d'une base et
est l'aire d'une base et 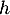 la hauteur relative à cette base.
la hauteur relative à cette base.
- Démontrer que (CO) est la hauteur du tétraèdre
- On admet que le triangle
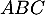 est rectangle en
est rectangle en 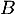 . Déduire des questions précédentes la distance du point
. Déduire des questions précédentes la distance du point 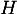 au plan
au plan 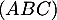 .
.
Correction exercice 3
Bac 2024, 5 points
-
- On a
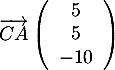 et
et
 et donc les produits scalaires
et donc les produits scalaires
![\[\overrightarrow{n_1}\cdot\overrightarrow{CA}=1\tm5+(-1)\tm5+0\tm(-10)=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/3.png)
et
![\[\overrightarrow{n_1}\cdot\overrightarrow{CD}=1\tm0+(-1)\tm0+0\tm\lp-\dfrac{25}2\rp=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/4.png)
Ainsi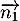 est orthogonal à deux vecteurs non colinéaires du plan (CAD), et est donc normal au plan (CAD).
est orthogonal à deux vecteurs non colinéaires du plan (CAD), et est donc normal au plan (CAD).
- Une équation cartésienne du plan (CAD) est donc de la forme
![\[1x+(-1)y+0z+d=0\iff x-y+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/6.png)
De plus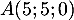 est un point de ce plan, et donc
est un point de ce plan, et donc
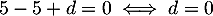 .
.
Ainsi, le plan (CAD) a bien pour équation cartésienne: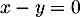 .
.
- On a
- On considère la droite
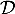 de représentation paramétrique
de représentation paramétrique
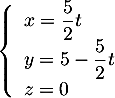 où
où 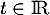 .
.
- Soit
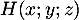 , alors il existe un réel
, alors il existe un réel 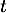 tel que
tel que
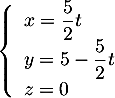 et de plus
et de plus 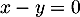 .
.
Ainsi,
![\[x=y \iff \dfrac52t=5-\dfrac52t \iff t=1\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/17.png)
et on trouve alors les coordonnées avec ce paramètre
![\[\la\begin{array}{l}x=\dfrac52\tm1=\dfrac52 \\ y=5-\dfrac52\tm1=\dfrac52 \\ z=0\enar\right.
\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/18.png)
soit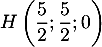 .
.
- On a
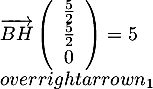 , c'est-à-dire que ces vecteurs sont colinéaires. En particulier, comme
, c'est-à-dire que ces vecteurs sont colinéaires. En particulier, comme 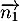 est normal au plan (CAD),
est normal au plan (CAD), 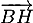 est aussi normal à ce plan.
est aussi normal à ce plan.
Comme ce plus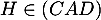 , on en déduit que
, on en déduit que 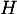 est le projeté orthogonal de
est le projeté orthogonal de 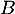 sur le plan (CAD).
sur le plan (CAD).
- Soit
-
- On peut soit calculer le produit scalaire
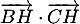 , ou alors utiliser le résultat précédent: comme
, ou alors utiliser le résultat précédent: comme 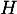 est le projeté orthogonal de
est le projeté orthogonal de 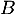 sur (CAD), on sait donc que
sur (CAD), on sait donc que 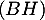 est orthogonale à toutes les droites du plan (CAD), en particulier orthogonale à (AH) puisque A et H appartiennent à (CAD).
est orthogonale à toutes les droites du plan (CAD), en particulier orthogonale à (AH) puisque A et H appartiennent à (CAD).
- L'aire du triangle
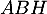 est
est
![\[\mathcal{A}_{ABH}=\dfrac12BH\times AH
\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/31.png)
avec
![\[BH=\sqrt{\lp\dfrac52\rp^2+\lp-\dfrac52\rp^2+0^2}=\dfrac52\sqrt2\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/32.png)
et
![\[AH=\sqrt{\lp-\dfrac52\rp^2+\lp-\dfrac52\rp^2+0^2}=\dfrac52\sqrt2\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/33.png)
d'où
![\[\mathcal{A}_{ABH}=\dfrac12\tm\dfrac52\sqrt2\tm\dfrac52\sqrt2=\dfrac{25}{4}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/34.png)
- On peut soit calculer le produit scalaire
-
-
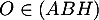 car le plan (ABH) est le plan d'équation
car le plan (ABH) est le plan d'équation 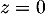 .
.
De plus (OC) est bien orthogonale à ce plan, car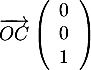 est un vecteur normal au plan d'équation
est un vecteur normal au plan d'équation 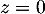 .
Ainsi, (CO) est bien la hauteur du tétraèdre
.
Ainsi, (CO) est bien la hauteur du tétraèdre 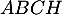 issue de
issue de 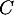 .
.
- Le volume du tétraèdre
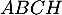 est
est
![\[\begin{array}{ll}V&=\dfrac13\mathcal{B} h\\[.8em]
&=\dfrac13\mathcal{A}_{ABH}\times OC\\[.8em]
&=\dfrac13\tm\dfrac{25}4\tm10\\[.8em]
&=\dfrac{125}6\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/42.png)
-
- En calculant le même volume d'une autre façon, on a
![\[V=\dfrac13\mathcal{A}_{ABC}h\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/43.png)
où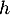 est la distance recherchée du point H au plan (ABC), et
est la distance recherchée du point H au plan (ABC), et
![\[\mathcal{A}_{ABC}=\dfrac12BC\times BA\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/45.png)
avec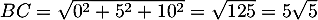 et
et
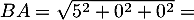 d'où
d'où
![\[\mathcal{A}_{ABC}=\dfrac12\tm5\sqrt5\tm5=\dfrac{25\sqrt5}2\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/48.png)
et donc
![\[V=\dfrac{125}6=\dfrac13\tm\dfrac{25\sqrt5}2h\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/49.png)
d'où
![\[h=\dfrac5{\sqrt5}=\sqrt5\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac19062024_c/50.png)
Cacher la correction
Exercice 4: Fonction logarithme: variations, limites, convexité et intégrale: calcul de l'aire entre deux courbes
Partie A : étude de la fonction 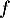
La fonction
-
- Déterminer, en justifiant, les limites de
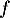 en 0 et en
en 0 et en 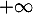 .
.
- Montrer que pour tout
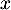 appartenant à
appartenant à ![$] 0$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/13.png) ;
; 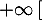 , on a :
, on a : 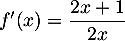 .
.
- Étudier le sens de variation de
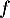 sur
sur ![$] 0 ;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/17.png) .
.
- Étudier la convexité de
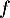 sur
sur ![$] 0 ;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/19.png) .
.
- Déterminer, en justifiant, les limites de
-
- Montrer que l'équation
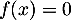 admet dans
admet dans ![$] 0 ;+\infty$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/21.png) [ une solution unique qu'on notera
[ une solution unique qu'on notera 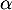 et justifier que
et justifier que 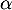 appartient à l'intervalle
appartient à l'intervalle ![$[1 ; 2]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/24.png) .
.
- Déterminer le signe de
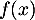 pour
pour ![$x \in] 0 ;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/26.png) .
.
- Montrer que
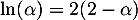 .
.
- Montrer que l'équation
Partie B : étude de la fonction 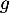
La fonction
On admet que la fonction
- Calculer
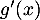 pour
pour ![$x \in] 0 ; 1]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/36.png) puis vérifier que
puis vérifier que 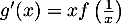 .
.
-
- Justifier que pour
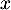 appartenant à l'intervalle
appartenant à l'intervalle ![$] 0 ; \frac1\alpha\left[\right.$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/39.png) , on a
, on a 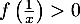 .
.
- On admet le tableau de signes suivant :
![\[ \renewcommand{\arraystretch}{1.4}
\begin{tabular}{|c|ccccc|}\hline
$x$ & 0 && $\frac1\alpha$ && 1 \\
\hline
Signe de $f\lp\frac{1}{x}\rp$ && $+$ & 0 & $-$& \\\hline
\end{tabular}
\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/41.png)
- Justifier que pour
Partie C : un calcul d'aire
On a représenté sur le graphique ci-dessous :
- La courbe
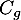 de la fonction
de la fonction 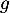 ;
;
- La parabole
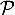 d'équation
d'équation 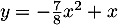 sur l'intervalle
sur l'intervalle ![$\left.] 0 ; 1\right]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/46.png) .
.
![\[\psset{unit=10cm,arrowsize=7pt}
\begin{pspicture*}(-.4,-.2)(1.2,.5)
\newcommand{\fctg}[1]{-7 8 div #1 2 exp mul #1 add
-0.25 #1 2 exp mul #1 ln mul
add}
\newcommand{\fctP}[1]{-7 8 div #1 2 exp mul #1 add}
\pscustom{
\psplot{.58}{1}{\fctg{x}} \gsave
\psplot{1}{.58}{\fctP{x}}
\fill[fillstyle=hlines,fillcolor=lightgray]
%\fill[fillstyle=vlines]
\grestore}
\psline{->}(-.05,0)(1.2,0)
\psline{->}(0,-.05)(0,.5)
\newcommand{\divdx}[1]{#1 10 div}
\multido{\i=0+1}{11}{\psline(! \divdx{\i} \space .01)(! \divdx{\i} \space -.01)
\psline[linestyle=dotted](! \divdx{\i} \space -.01)(! \divdx{\i} \space .5)}
\multido{\i=1+1}{4}{\psline(! .01 \space \divdx{\i})(! -.01 \space \divdx{\i})
\psline[linestyle=dotted](! .01 \space \divdx{\i})(! 1.1 \space \divdx{\i})}
\psplot{.001}{1}{\fctg{x}}
\psplot{.001}{1}{\fctP{x}}
\psline[linestyle=dashed](.58,0)(.58,.33)
\rput(-.02,-.02){$O$}
\rput[r](-.02,.1){$0,1$}
\rput(.1,-.04){$0,1$}
\rput(.58,-.04){$\frac1\alpha$}
\psline[linestyle=dashed](1,0)(1,.12)
\rput(1,-.04){$1$}
\rput[l](.72,.33){$\mathcal{C}_g$}
\rput[l](.72,.23){$\mathcal{P}$}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/47.png)
On souhaite calculer l'aire
On rappelle que
-
- Justifier la position relative des courbes
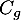 et
et 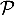 sur l'intervalle
sur l'intervalle ![$] 0 ; 1]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/56.png) .
.
- Démontrer l'égalité :
![\[\int_{\frac1\alpha}^1 x^2 \ln x dx = \frac{-\alpha^{3}-6 \alpha+13}{9 \alpha^{3}}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024/57.png)
- Justifier la position relative des courbes
- En déduire l'expression en fonction de
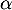 de l'aire
de l'aire 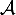 .
.
Correction exercice 4
Bac 2024, 6 points
Partie A : étude de la fonction 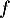
La fonction
-
- On a
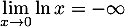 et donc,
et donc,
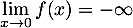 .
.
De même,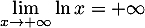 , et donc, par addition des limites,
, et donc, par addition des limites, 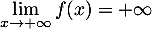
- On a
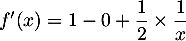 soit, en mettant sur le même dénominateur
soit, en mettant sur le même dénominateur 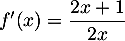 .
.
- Grâce à la question précédente, on peut alors dresser le tableau de variation:
![\[\begin{tabular}{|c|ccc|}\hline
$x$ & 0 &\hspace*{1em}&$+\infty$ \\\hline
$2x+1$ && $+$ & \\\hline
$2x$ &0& $+$ & \\\hline
$f'(x)$ && $+$ & \\\hline
&&&$+\infty$\\
$f$&\psline(-.1,1.4)(-.1,-.65)\psline(0,1.4)(0,-.65)&\Large{$\nearrow$}&\\
&\qquad $-\infty$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/16.png)
- La convexité est donnée par le signe de la dérivée seconde.
On a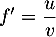 avec
avec 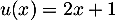 donc
donc 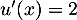 et
et 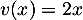 donc
donc 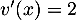 .
.
On a alors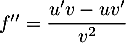 , soit
, soit
![\[f''=\dfrac{2(2x)-(2x+1)2}{(2x)^2}=\dfrac{-1}{2x^2}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/23.png)
On trouve donc que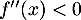 donc que
donc que 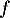 est concave sur
est concave sur ![$]0;£\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/26.png) .
.
- On a
-
-
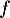 est continue et strictement croissante sur
est continue et strictement croissante sur ![$]0;+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/28.png) avec
avec
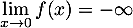 et
et
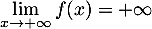 .
.
On en déduit d'après le théorème de la bijection (ou corolloaire du théorème des valeurs intermédiaires) qu'il existe une unique solution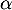 à l'équation
à l'équation 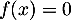 .
.
De plus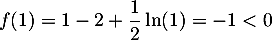 et
et 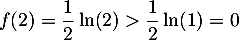 , ce qui montre que, plus précisément,
, ce qui montre que, plus précisément, ![$\alpha\in]1;2[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/35.png) .
.
- D'après les questions précédentes, comme
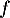 est strictement croissante et s'annule en
est strictement croissante et s'annule en 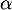 , on a nécessairement les signes:
, on a nécessairement les signes:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & 0 && $\alpha$ &&$+\infty$ \\\hline
$f(x)$ &\psline(0,.35)(0,-.15)\,\psline(0,.35)(0,-.15)& $-$ &\mbox{$0\hspace{-0.67em}\mid$} &$+$ & \\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/38.png)
- Par définition, on a
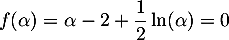 , c'est-à-dire, en isolant
, c'est-à-dire, en isolant 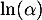 , que
, que
![\[\ln(\alpha)=2(2-\alpha)\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/41.png)
-
Partie B : étude de la fonction 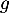
-
![\[\begin{array}{ll}g'(x)&=-\dfrac78\tm2x+1-\dfrac14\left( 2x\ln x+x^2\tm\dfrac1x\rp\\[1em]
&=-\dfrac74x+1-\dfrac12x\ln x-\dfrac14x\\[.8em]
&=-2x+1-\dfrac12\ln x
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/43.png)
Par ailleurs, on calcule
![\[\begin{array}{ll}xf\lp\frac1x\rp&=x\lp\dfrac1x-2+\dfrac12\ln\lp\dfrac1x\rp\rp\\[1em]
&=1-2x-\dfrac12\ln x
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/44.png)
et on trouve donc bien finalement que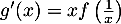 .
.
-
- Pour
![$x\in\left] 0 ; \frac1\alpha\right[$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/46.png) , on a
, on a
![\[\begin{array}{ll}x<\dfrac1\alpha&\iff \dfrac1x>\alpha\\
&\iff f\lp\dfrac1x\rp>f(\alpha)=0
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/47.png)
car on a montré que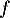 est strictement croissante sur
est strictement croissante sur 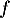 sur
sur 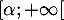 .
.
- On admet le tableau de signes suivant :
![\[ \renewcommand{\arraystretch}{1.4}
\begin{tabular}{|c|ccccc|}\hline
$x$ & 0 && $\frac1\alpha$ && 1 \\
\hline
$f\lp\frac{1}{x}\rp$ && $+$ & 0 & $-$& \\\hline
$x$ & 0 & $+$ &$|$ & $+$& \\\hline
$g'(x)=xf'\lp\frac1x\rp$ & & $+$ & 0 & $-$ & \\\hline
&&&&&\\
$g$&\psline(0,1.9)(0,-.9)\,\psline(0,1.9)(0,-.9)&\large{$\nearrow$}&&\large{$\searrow$}&\\
&&&&&\\\hline
\end{tabular}
\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/51.png)
- Pour
Partie C : un calcul d'aire.
-
- On note la différence
![\[\begin{array}{ll}d(x)&=g(x)-\lp\dfrac78x^2+x\rp\\
&=-\dfrac14x^2\ln x
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/52.png)
Or, pour![$x\in]0;1@$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/53.png) , on a
, on a 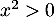 et
et 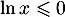 , et ainsi
, et ainsi 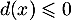 , ce qui signifie que
, ce qui signifie que 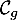 est au-dessus de
est au-dessus de 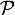 sur
sur ![$]0;1]$](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/59.png) .
.
- On utilise une intégration par partie en dérivant le logarithme:
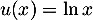 donc
donc 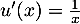 , et
, et 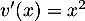 donc
donc 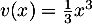 , et alors
, et alors
![\[\begin{array}{ll}I&=\dsp\int_{\frac1\alpha}^1 \ln x\, x^2 dx\\[1.2em]
&=\dsp\left[ \ln x\times \dfrac13x^3\rb_{\frac1\alpha}^1-\int_{\frac1\alpha}^1\dfrac1x\times\dfrac13x^3 dx\\[1.2em]
&=\dsp0-\ln\lp\dfrac1\alpha\rp\dfrac1{3\alpha^3}
-\dfrac13\int_{\frac1\alpha}^1x^2 dx\\[1.2em]
&=\dfrac{\ln\alpha}{3\alpha^3}-\dfrac13\lb\dfrac{x^3}3\rb_{\frac1\alpha}^1\\[1.2em]
&=\dfrac{\ln\alpha}{3\alpha^3}-\dfrac19\lp1-\dfrac1{\alpha^3}\right)
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/64.png)
et donc, en se rappelant que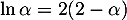 , et en mettant sur le même dénominateur
, et en mettant sur le même dénominateur
![\[\begin{array}{ll}I&=\dfrac{3\tm2(2-\alpha)-(\alpha^2-1)}{9\alpha^2}\\[.8em]
&=\dfrac{-\alpha^3-6 \alpha+13}{9 \alpha^3}\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/66.png)
- On note la différence
- On en déduit l'aire recherchée:
![\[\begin{array}{ll}\mathcal{A}&=\dsp\int_{\frac1\alpha}^1\left( g(x)-\left(-\dfrac78x^2+x\rp\rp dx\\[1.4em]
&=\dsp\int_{\frac1\alpha}^1\lp-\dfrac14x^2\ln x\right) dx\\[1.2em]
&=-\dfrac14I = \dfrac{\alpha^3+6 \alpha-13}{36 \alpha^3}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/exBac19062024_c/67.png)
Cacher la correction
Quelques autres devoirs
Voir aussi: