Oral du bac: suites, récurrence - géométrie dans l'espace
suites, géométrie dans l'espace
- L'utilisation d'une calculatrice est autorisée.
- La qualité des raisonnements, de l'expression, et la précision des justifications prendront une part importante dans l'appréciation de l'interrogation orale.
- Il s'agit d'une épreuve orale: il n'est pas indispensable de rédiger l'ensemble des réponses, des calculs, du raisonnement …
Par contre vous devez être en mesure d'apporter toutes les justifications nécessaires.
L'exposé de la méthode et du raisonnement sera pris en compte.
Exercice 1: Suite récurrente, démonstration par récurrence et calcul de limite
Soit 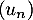 la suite défnie par
la suite défnie par  et, pour tout entier
et, pour tout entier 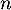 ,
,
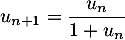 .
.
- Calculer
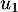 et
et 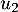 .
.
- Démontrer que, pour tout entier
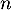 ,
,
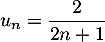 .
.
- Déterminer la limite de cette suite.
Correction exercice 1
Cacher la correction
-
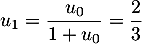 et
et 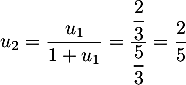 .
.
- On peut démontrer cette propriété par récurrence.
Initialisation: La propriété est vraie pour car
car
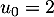 et
et 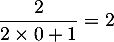 .
.
Hérédité: Supposons que la propriété soit vraie à un certain rang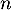 , c'est-à-dire que
, c'est-à-dire que
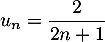 ,
,
alors, au rang suivant, on a
![\[\begin{array}{ll}u_{n+1}&=\dfrac{u_n}{1+u_n}
=\dfrac{\dfrac2{2n+1}}{1+\dfrac2{2n+1}}
=\dfrac{\dfrac2{2n+1}}{\dfrac{2n+3}{2n+1}}\\[2.2em]
&=\dfrac2{2n+3}
=\dfrac2{2(n+1)+1}\enar\]](/Generateur-Devoirs/TS/ChapSuites/exOralrec_c/8.png)
ce qui montre que la propriété est encore vraie au rang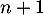 suivant.
suivant.
Conclusion: D'après le principe de récurrence, la propriété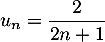 est donc vraie pour tout entier
est donc vraie pour tout entier 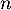 .
.
- On a donc
![\[u_n=\dfrac2{2n+1}
=\dfrac2{2n\lp1+\frac1{2n}\right)}
=\dfrac1{n}\tm\dfrac1{1+\frac1{2n}}\]](/Generateur-Devoirs/TS/ChapSuites/exOralrec_c/12.png)
et donc, comme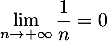 et
et
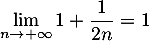 , on obtient
, on obtient
![\[\lim_{n\to+\infty}u_n=0\]](/Generateur-Devoirs/TS/ChapSuites/exOralrec_c/15.png)
Cacher la correction
Exercice 2: Intersection dans l'espace d'une droite et d'un plan
Dans l'espace muni d'un repère orthonormé, on considère les points 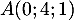 ,
, 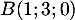 ,
,  et
et 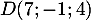 , ainsi que
la droite
, ainsi que
la droite  passant par le point
passant par le point 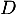 et de vecteur directeur
et de vecteur directeur 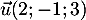 .
.
- Démontrer que les points
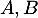 et
et 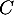 ne sont pas alignés.
ne sont pas alignés.
- Démontrer que la droite
 est orthogonale au plan
est orthogonale au plan 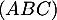 .
et en déduire une équation cartésienne du plan
.
et en déduire une équation cartésienne du plan 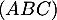 .
.
- Déterminer une représentation paramétrique de la droite
 .
.
- Déterminer les coordonnées du point
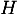 , intersection de la droite
, intersection de la droite  et du plan
et du plan 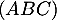
Correction exercice 2
Cacher la correction
-
 et
et 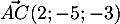 .
Ces coordonnées ne sont pas proportionnelles, et donc ces vecteurs ne sont donc pas colinéaires.
.
Ces coordonnées ne sont pas proportionnelles, et donc ces vecteurs ne sont donc pas colinéaires.
On en déduit que les points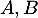 et
et 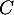 ne sont pas alignés (et définissent alors un plan).
ne sont pas alignés (et définissent alors un plan).
-
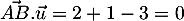 et
et 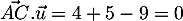 .
.
Le vecteur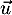 est donc orthogonal à deux vecteurs non colinéaires du plan
est donc orthogonal à deux vecteurs non colinéaires du plan 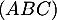 : c'est donc un vecteur normal au plan
: c'est donc un vecteur normal au plan 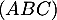 .
.
La droite est par conséquent orthogonale au plan
est par conséquent orthogonale au plan 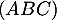 .
.
Une équation cartésienne du plan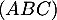 est donc de la forme
est donc de la forme 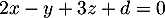 .
.
Le point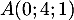 appartient au plan
appartient au plan 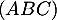 , et donc
, et donc 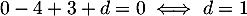 .
.
Ainsi une équation cartésienne du plan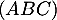 est
est 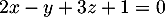 .
.
- La droite
 passe par le point
passe par le point 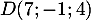 et a pour vecteur directeur
et a pour vecteur directeur 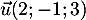 .
.
Une représentation paramétrique de la droite est donc:
est donc:
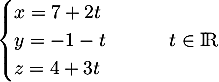 .
.
- Les coordonnées du point
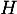 sont solution du système:
sont solution du système:
![\[\begin{array}{ll}
\la\begin{array}{ll}x=7+2t\\y=-1-t\\z=4+3t\\2x-y+3z+1=0\enar\right.
&\iff\la\begin{array}{l}x=7+2t\\y=-1-t\\z=4+3t\\2(7+2t)-(-1-t)+3(4+3t)+1=0\enar\right.\\[2.5em]
&\iff\la\begin{array}{l}x=7+2t\\y=-1-t\\z=4+3t\\28+14t=0\enar\right. \\[2.5em]
&\iff\la\begin{array}{ll}x=7+2t\\y=-1-t\\z=4+3t\\t=-2\enar\right.\\[2.5em]
&\iff\la\begin{array}{ll}x=3\\y=1\\z=-2\\t=-2\enar\right.\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/exOralInter_c/25.png)
Donc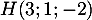 .
.
Cacher la correction
Voir aussi: