Probabilité de vente d'un produit, semaine après semaine
Exercice corrigé - Spécialité maths, terminale générale
Un commerçant étudie l'évolution des ventes d'un de ses produits afin de pouvoir anticiper ses commandes.
Une étude auprès de ses clients montre que:
On choisit au hasard un client ayant acheté ce produit au cours de la semaine 1 et, pour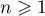 , on note
, on note 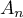 l'événement:
"le client achète le produit au cours de la semaine
l'événement:
"le client achète le produit au cours de la semaine 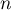 ",
et
",
et 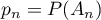 sa probabilité.
On a ainsi
sa probabilité.
On a ainsi 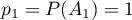 .
.
- parmi les clients qui achètent ce produit une semaine donnée, 90% d'entre eux achètent aussi ce produit la semaine suivante;
- permi les clients qui n'achètent pas ce produit une semaine donnée, 60% d'entre eux n'achètent pas ce produit la semaine suivante.
On choisit au hasard un client ayant acheté ce produit au cours de la semaine 1 et, pour
-
- Reproduire et compléter l'arbre de probabilités ci-dessous, relatif aux trois premières semaines.
![\[\psset{xunit=1.3cm,yunit=1cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\rput(0,0){$A_1$}
\psline(.2,.2)(1.5,1)\rput(1.75,1){$A_2$}
\psline(.2,-.2)(1.5,-1)\rput(1.75,-1){$\overline{A_2}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$A_3$}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{A_3}$}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{A_3}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$A_3$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine/6.png)
- Démontrer que
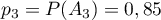 .
.
- Reproduire et compléter l'arbre de probabilités ci-dessous, relatif aux trois premières semaines.
- Démontrer que, pour tout entier
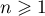 , on a
, on a
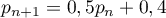 .
.
- On pose, pour tout entier
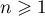 ,
, 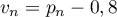 .
.
- Démontrer que
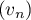 est une suite géométrique.
est une suite géométrique.
- Exprimer
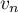 , puis
, puis 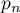 , en fonction de
, en fonction de 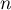 .
.
- Déterminer la limite de la suite
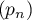 .
Interpréter ce résultat dans le contexte de l'exercice.
.
Interpréter ce résultat dans le contexte de l'exercice.
- Démontrer que
Correction
Cacher la correction
-
- Reproduire et compléter l'arbre de probabilités ci-dessous, relatif aux trois premières semaines.
![\[\psset{xunit=1.3cm,yunit=1cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\rput(0,0){$A_1$}
\psline(.2,.2)(1.5,1)\rput(1.75,1){$A_2$}
\rput(.8,.9){90\%}
\psline(.2,-.2)(1.5,-1)\rput(1.75,-1){$\overline{A_2}$}
\rput(.8,-1){10\%}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$A_3$}
\rput(2.8,1.6){90\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{A_3}$}
\rput(2.8,.3){10\%}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{A_3}$}
\rput(2.8,-1.6){60\%}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$A_3$}
\rput(2.8,-.4){40\%}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine_c/1.png)
-
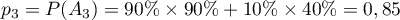 .
.
- Reproduire et compléter l'arbre de probabilités ci-dessous, relatif aux trois premières semaines.
- En reprenant et adaptant l'arbre précédent, on a
![\[\psset{xunit=1.3cm,yunit=1cm}
\begin{pspicture}(-.4,-2)(4.2,2)
%\rput(0,0){$A_1$}
\psline(.2,.2)(1.5,1)\rput(1.75,1){$A_n$}
\rput(.8,.9){$p_n$}
\psline(.2,-.2)(1.5,-1)\rput(1.75,-1){$\overline{A_n}$}
\rput(.8,-1){$1-p_n$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$A_{n+1}$}
\rput(2.8,1.6){90\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{A_{n+1}}$}
\rput(2.8,.3){10\%}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{A_{n+1}}$}
\rput(2.8,-1.6){60\%}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$A_{n+1}$}
\rput(2.8,-.4){40\%}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine_c/3.png)
et alors
![\[p_{n+1}=0,9p_n+0,4(1-p_n)=0,5p_n+0,4\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine_c/4.png)
-
- Pour tout entier
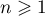 ,
,
![\[\begin{array}{ll}v_{n+1}&=p_{n+1}-0,8\\
&=0,5p_n+0,4-0,8\\
&=0,5p_n-0,4\\
&=0,5\left( p_n-0,8\rp=0,5v_n\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine_c/6.png)
ce qui montre que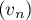 est une suite géométrique de raison
est une suite géométrique de raison 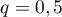 .
.
- On en déduit que, pour tout entier
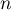 ,
,
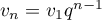 , soit, avec
, soit, avec 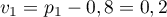
![\[v_n=0,2\tm0,5^n\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine_c/12.png)
puis
![\[v_n=p_n-0,8\iff p_n=v_n+0,8=0,2\tm0,5^n+0,8\]](/Generateur-Devoirs/TS/ChapProbabilites/Probabilite-ventes-semaine-apres-semaine_c/13.png)
- Comme
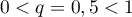 , on a
, on a 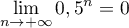 et donc
et donc 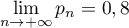 .
Au bout d'un grand nombre de semaines, la probabilité qu'un client achète
ce produit tend vers 80%, ou encore qu'il achètera ce produit 8 semaines sur 10.
.
Au bout d'un grand nombre de semaines, la probabilité qu'un client achète
ce produit tend vers 80%, ou encore qu'il achètera ce produit 8 semaines sur 10.
- Pour tout entier
Cacher la correction
Tag:Probabilités
Voir aussi:
