Oral de Bac - Variation d'une primitive - Encadrements d'intégrales

Exercice corrigé - Spécialité maths, terminale générale

Soit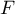

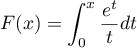la fonction définie sur $$]0;+\infty[$ par $$\displaystyle F(x)=\int_0^x\dfrac{e^t}{t}dt$ .

Déterminer le sens de variation de .
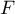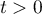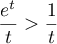Prouver que, pour tout , $$\dfrac{e^t}{t}>\dfrac1t$ .
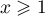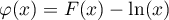En déduire, pour $$x\geqslant 1$ , le signe de $$\varphi(x)=F(x)-\ln(x)$ .
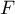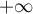Déduire de cette étude le comportement de en $$+\infty$ .

Correction

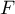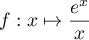est la primitive qui s'annule en 1 de la fonction $$f:x\mapsto \dfrac{e^x}{x}$ .
En d'autres termes, on a et .
En particulier, comme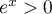 sur $$\R$ , on a $$F'(x)=f(x)=\dfrac{e^x}{x}>0$ sur $$]0;+\infty[$ , ce qui montre que 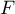est strictement croissante.
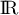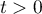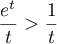Comme la fonction exponentielle est strictement croissante sur $$\R$ , on a $$t>0\iff e^t>e^0=1$ , et donc, en divisant par , $$\dfrac{e^t}{t}>\dfrac{1}{t}$ .

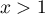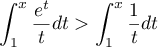Comme l'intégrale conserve l'ordre, pour , on a alors $$\dsp\int_1^x\dfrac{e^t}{t}dt>\int_1^x\dfrac1tdt$ .
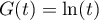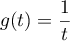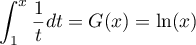Or $$G(t)=\ln(t)$ est la primitive qui s'annule en 1 de $$g(t)=\dfrac1t$ , et donc $$\dsp\int_1^x\dfrac1tdt=G(x)=\ln(x)$ .
On a ainsi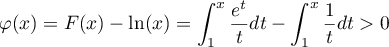 $$\dsp\varphi(x)=F(x)-\ln(x)=\int_1^x\dfrac{e^t}{t}dt-\int_1^x\dfrac1tdt>0$
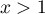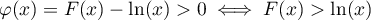Pour , on a donc $$\varphi(x)=F(x)-\ln(x)>0\iff F(x)>\ln(x)$ .
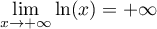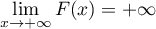Or, $$\dsp\lim_{x\to+\infty}\ln(x)=+\infty$ , et donc d'après le corollaire du théorème des gendarmes, $$\dsp\lim_{x\to+\infty}F(x)=+\infty$ .

Tag:Intégrales

Autres sujets au hasard:

Voir aussi: