Oral de Bac - Équation du 2nd degré en exponentielle
Exercice corrigé - Spécialité maths, terminale générale
- Résoudre dans
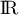 l'équation
l'équation 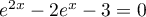 .
.
(on pourra utiliser le changement de variable )
)
- Étudier le sens de variation de la fonction
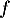 définie sur
définie sur 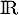 par
par 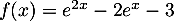 .
.
Tracer l'allure de sa courbe représentative.
Correction
Cacher la correction
- Soit
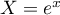 , alors
, alors 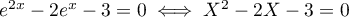 .
Cette équation du second degré admet deux solutions réelles
.
Cette équation du second degré admet deux solutions réelles 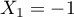 et
et  .
.
On revient ensuite à l'inconnue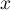 :
:
-
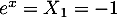 n'a pas de solution, une exponentielle étant toujours
strictement positive;
n'a pas de solution, une exponentielle étant toujours
strictement positive;
-
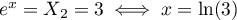 .
.
 a donc comme unique solution rélle
a donc comme unique solution rélle 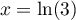 .
.
-
- On a
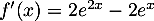 .
.
On cherche le signe de cette dérivée, donc à résoudre
![\[\begin{array}{ll}f'(x)>0\iff 2e^{2x}-2e^x>0
&\iff e^{2x}>e^x\\
&\iff 2x>x\\
&\iff x>0\enar\]](/Generateur-Devoirs/TS/ChapExponentielle/exOral01_c/11.png)
et on a donc
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-\infty$ &&$0$&& $+\infty$ \\\hline
$f'(x)$ && $-$ &\zb& $+$ &\\\hline
&&&&&\\
$g$ && \Large{$\searrow$}&&
\Large{$\nearrow$}&\\
&&&$-4$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/exOral01_c/12.png)
et la courbe qui va avec (sur laquelle on n'oublie pas de situer la solution trouvée à la question précédente):
{\i}
}
\psplot{-5}{5}{2.718 x 2 mul exp -2 2.178 x exp mul add -3 add}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/exOral01_c/13.png)
Cacher la correction
Tag:Exponentielle
Voir aussi:
