Logarithme composé avec fraction rationnelle, et asymptote oblique
Exercice corrigé - Spécialité maths, terminale générale
Soit  la fonction définie sur
la fonction définie sur ![$]\,0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/ex1/2.png) par:
par:
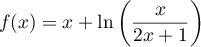 .
.
On note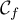 sa courbe représentative dans un repère
sa courbe représentative dans un repère
 .
.
On note
- Etudier les limites de
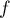 en
en 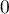 et en
et en 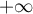 .
.
- Etudier les variations de
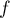 et dresser son tableau de
variation.
et dresser son tableau de
variation.
-
- Montrer que la droite
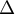 d'équation
d'équation  est
asymptote à
est
asymptote à 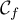 en
en  .
.
- Etudier la position de
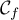 par rapport à
par rapport à 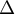 .
.
- Montrer que la droite
- Montrer que l'équation
 admet une solution unique
admet une solution unique
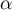 et justifier que
et justifier que  .
.
- Tracer
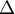 et
et 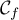 .
.
Correction
Soit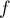 la fonction définie sur
la fonction définie sur ![$]\,0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/ex1_c/2.png) par:
par:
 .
.
Cacher la correction
Soit
-
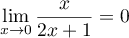 , et donc, par composition des
limites
, et donc, par composition des
limites
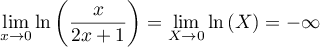 .
.
Ainsi, par addition des limites,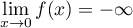 .
.
 ,
,
et donc, par composition des limites,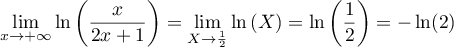 .
.
Enfin, par addition des limites,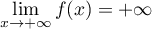 .
.
- Pour tout
 ,
,
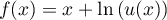 , donc
, donc
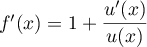 ,
,
avec , et donc
, et donc
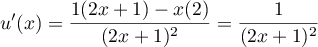 .
.
Ainsi, pour tout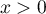 ,
,
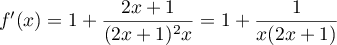 .
.
Pour tout ,
, 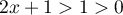 , et donc,
, et donc,  ,
d'où,
,
d'où,  .
.
Ainsi,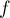 est strictement croissante sur
est strictement croissante sur ![$]0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/ex1_c/22.png) .
.
![{|c|ccc|}\hline
$x$ & $0$ &\hspace*{1.2cm}& $+\infty$ \\\hline
&&&$+\infty$ \\
$f$ && \psline[arrowsize=7pt]{->}(-0.9,-0.4)(0.9,0.4)& \\
&$-\infty$&& \\\hline](/Generateur-Devoirs/TS/ChapLogarithme/ex1_c/23.png)
-
- Pour tout
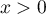 ,
,
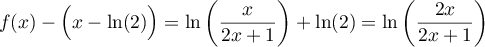 .
.
Or, ,
,
et donc, par composition des limites,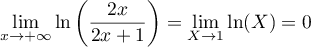 .
.
Ainsi,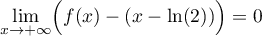 et la droite
et la droite 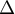 est asymptote oblique à
est asymptote oblique à  en
en
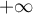 .
.
- On avait, pour tout
 ,
,
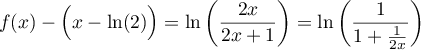 .
Pour tout
.
Pour tout  ,
, 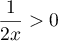 ,
et donc,
,
et donc, 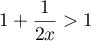 ,
d'où
,
d'où  et donc,
et donc,
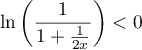
Ainsi,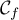 est toujours au dessous de
est toujours au dessous de 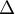 .
.
- Pour tout
-
 est continue sur
est continue sur ![$]0;+\infty[](/Generateur-Devoirs/TS/ChapLogarithme/ex1_c/42.png) , strictement croissante,
et
, strictement croissante,
et 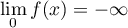 et
et
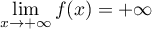 .
.
Ainsi, d'après le théorème de la bijection (ou théorème des valeurs intermédiaires version forte), il existe un unique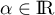 solution de l'équation
solution de l'équation
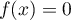 .
.
De plus,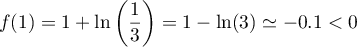 et
et
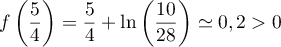 .
Ainsi, d'après le même théorème,
on a bien
.
Ainsi, d'après le même théorème,
on a bien 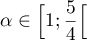 .
.
-
![\psset{unit=1.2cm,arrowsize=7pt}
\begin{pspicture}(-0.5,-3.5)(5,4.3)
\psline{->}(-0.5,0)(5,0)
\psline{->}(0,-3.5)(0,4.3)
\psplot[plotpoints=1000]{0.035}{5}{x 2 x mul 1 add div ln x add}
\rput(0.7,-1.3){$\mathcal{C}_f$}
\psplot{-0.6}{5.}{x 2 ln sub}\rput(-0.3,-1.3){$\Delta$}
\psline(1.12,0.1)(1.12,-0.1)\rput(1.2,-0.25){$\alpha$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapLogarithme/ex1_c/50.png)
Cacher la correction
Tag:Logarithme
Voir aussi:
