Fonction rationnelle en exponentielle
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 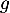 définie sur
définie sur 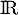 par
par 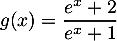 .
.
- Déterminer les limites en
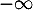 et
et 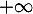 de
de 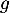 .
Interpréter graphiquement ces résultats.
.
Interpréter graphiquement ces résultats.
- Étudier le sens de variation de
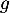 .
.
- Tracer l'allure de la courbe de
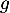 .
.
Correction
On considère la fonction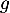 définie sur
définie sur  par
par 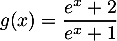 .
.
Cacher la correction
On considère la fonction
- On a
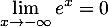 d'où
d'où
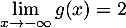 .
.
En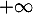 , on a
, on a
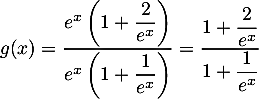 avec
avec 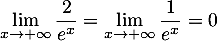 d'où
d'où 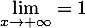 .
.
On en déduit que les droites d'équations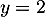 et
et 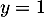 sont des asymptotes verticales à la courbe de
sont des asymptotes verticales à la courbe de 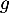 , respectivement en
, respectivement en 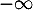 et
et 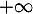 .
.
- On a
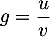 avec
avec 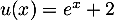 , donc
, donc 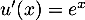 et
et 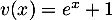 , donc
, donc 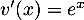 .
On obtient alors
.
On obtient alors
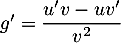 soit
soit
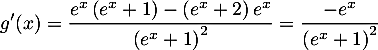
![\[\begin{tabular}{|c|ccc|}\hline
$x$ & $-\infty$ && $+\infty$ \\\hline
$-e^x$ && $-$ &\\\hline
$\left( e^x+1\rp^2$ && $+$ &\\\hline
$g'(x)$ && $-$ &\\\hline
&2&&\\
$g$&&\Large{$\searrow$}&\\
&&&1\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex00.5_c/22.png)
- On trace alors l'allure de la courbe,
avec ses asymptotes
![\[\psset{xunit=2cm,yunit=1.8cm,arrowsize=8pt}
\begin{pspicture*}(-3.5,-.6)(3.5,2.7)
\psline{->}(-3.5,0)(3.5,0)
\psline{->}(0,-1)(0,2.7)
\psplot[linewidth=1.7pt]{-3.5}{3.5}{2.718 x exp 2 add 2.718 x exp 1 add div}
\rput(1.2,1.4){$\mathcal{C}_f$}
\psline[linecolor=blue](-4,2)(4,2)\rput(-1,2.2){\blue$y=2$}
\psline[linecolor=blue](-4,1)(4,1)\rput(-1,.8){\blue$y=1$}
\rput(-.1,-.2){0}
\psline(-.1,1.5)(.1,1.5)\rput[l](.1,1.6){\small1,5}
\end{pspicture*}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex00.5_c/23.png)
Cacher la correction
Tag:Exponentielle
Voir aussi:
