fonction logistique à étudier
Exercice corrigé - Spécialité maths, terminale générale
On considère l'équation différentielle
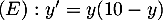 , avec la condition
, avec la condition 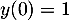 .
.
On définit la fonction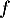 définie sur
définie sur  par
l'expression
par
l'expression
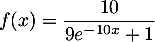 .
.
On définit la fonction
- Montrer que
 est solution de l'équation
est solution de l'équation 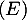 .
.
- Déterminer la limite de
 en
en  ,
et interpréter, si possible, graphiquement.
,
et interpréter, si possible, graphiquement.
- Étudier le sens de variation de
 .
.
- Montrer que, pour tout réel
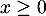 , on a
, on a
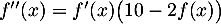 .
.
En déduire la convexité de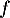 .
.
- Tracer l'allure de la courbe de
 en expolitant tous les résultats précédents.
en expolitant tous les résultats précédents.
Correction
Cacher la correction
- On a
 avec
avec
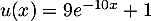 soit
soit 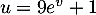 ,
donc
,
donc  , donc encore
, donc encore  ,
et donc
,
et donc
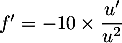 ,
soit
,
soit
![\[f'(x)=-10\dfrac{-90e^{-10x}}{\lp9e^{-10x}+1\rp^2}
=\dfrac{900e^{-10x}}{\lp9e^{-10x}+1\rp^2}
\]](/Generateur-Devoirs/TS/ChapEqDiff/logistiq_c/7.png)
D'utre part, on a
![\[\begin{array}{ll}f(x)\lp10-f(x)\right)
&=\dfrac{10}{9e^{-10x}+1}\lp10-\dfrac{10}{9e^{-10x}+1}\rp\\
&=\dfrac{10}{9e^{-10x}+1}\lp\dfrac{9e^{-10x}}{9e^{-10x}+1}\rp\\
&=\dfrac{900e^{-10x}}{\lp9e^{-10x}+1\rp^2}
\enar\]](/Generateur-Devoirs/TS/ChapEqDiff/logistiq_c/8.png)
On trouve donc bien que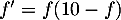 , c'est-à-dire que
, c'est-à-dire que 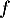 est solution de l'équation différentielle
est solution de l'équation différentielle
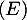 .
.
De plus,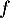 vérifie aussi la condition initiale
vérifie aussi la condition initiale 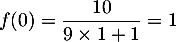 .
.
- On a
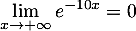 et donc
et donc
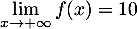 .
.
On en déduit que la droite d'équation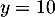 est asymptote horizontale
à la courbe de
est asymptote horizontale
à la courbe de  en
en  .
.
- À la première question, on a vu que
![\[f'(x)=\dfrac{900e^{-10x}}{\lp9e^{-10x}+1\rp^2}\]](/Generateur-Devoirs/TS/ChapEqDiff/logistiq_c/19.png)
et, comme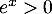 pour tout réel
pour tout réel 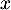 , on trouve que
, on trouve que
 , et donc que
, et donc que 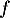 est strictement croissante sur
est strictement croissante sur  .
.
- La convexité de
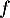 est donnée par le signe de sa dérivée seconde.
est donnée par le signe de sa dérivée seconde.
On peut soit calculer celle-ci à partir du résultat de la première question, soit utiliser le fait que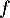 est solution de l'équation
est solution de l'équation 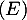 .
.
En effet, on sait que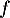 solution de
solution de 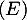 , c'est-à-dire que
, c'est-à-dire que
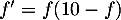 .
En dérivant cette relation, on obtient (en dérivant le produit)
.
En dérivant cette relation, on obtient (en dérivant le produit)
![\[f''=f'(10-f) + f(-f')=f'(10-f-f)=f'(10-2f)\]](/Generateur-Devoirs/TS/ChapEqDiff/logistiq_c/31.png)
On a vu que , et le signe de
, et le signe de 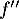 est donc donné par celui de
est donc donné par celui de
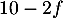 :
:
![\[\begin{array}{rl}10-2f(x)>0
\iff&f(x)<5\\
\iff&\dfrac{10}{9e^{-10x}+1}<5\\
\iff&\dfrac{9e^{-10x}+1}{10}>\dfrac15\\
\iff&9e^{-10x}+1>\dfrac{10}5=2\\
\iff&e^{-10x}>\dfrac19\\
\iff&-10x>\ln(1/9)=-\ln(9)\\
\iff&x<\dfrac{\ln(9)}{10}
\enar\]](/Generateur-Devoirs/TS/ChapEqDiff/logistiq_c/35.png)
On en déduit que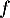 est convexe sur
est convexe sur 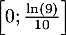 ,
et est concave sur
,
et est concave sur
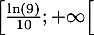
En particulier, le point d'abscisse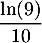 est
un point d'inflexion pour la courbe de
est
un point d'inflexion pour la courbe de  .
.
- On trace l'allure de la courbe avec, impérativement,
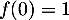 ,
, 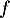 croissante, l'asymptote
croissante, l'asymptote 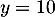 , et le point d'inflexion et la tangente en ce point (la courbe traverse la tangente en un point d'inflexion...):
, et le point d'inflexion et la tangente en ce point (la courbe traverse la tangente en un point d'inflexion...):
{1}
\psline(-.02,10)(1,10)
\rput[r](-0.025,10){10}
\psline[linestyle=dashed](0,5)(0.22,5)(0.22,0)
\rput[r](-.025,5){5}
\rput(.22,-.6){$\dfrac{\ln(9)}{10}$}
\psplot{0}{.4}{25 x 0.22 sub mul 5 add}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapEqDiff/logistiq_c/44.png)
Cacher la correction
Tag:Équations différentielles
Voir aussi:
