Fonction avec paramètres à déterminer, tangente, position relative
Exercice corrigé - Spécialité maths, terminale générale
D'après sujet de bac
Partie A
Soit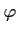 la fonction numérique de la variable réelle
la fonction numérique de la variable réelle 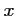 telle
que:
telle
que:
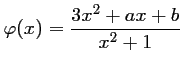 .
.
Déterminer les réels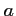 et
et  pour que la courbe représentative de
pour que la courbe représentative de
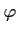 soit tangente au point
soit tangente au point 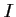 de coordonnées
de coordonnées 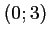 à la droite
à la droite
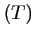 d'équation
d'équation 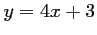 .
.
Partie B
Soit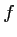 la fonction numérique de la variable réelle
la fonction numérique de la variable réelle 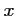 telle que:
telle que:
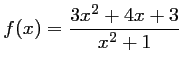 .
.
Correction
Partie A
Soit
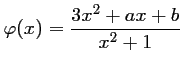 .
.
Déterminer les réels
Partie B
Soit
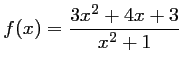 .
.
- Montrer que pour tout
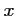 réel,
réel,
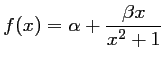 ,
,
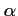 et
et  étant deux réels que l'on déterminera.
étant deux réels que l'on déterminera.
- Etudier la fonction
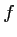 .
.
- Etudier la position de la courbe
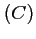 représentative de
représentative de 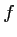 par
rapport à la tangente
par
rapport à la tangente 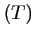 au point
au point 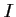 de coordonnées
de coordonnées 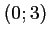 .
.
- Construire la courbe
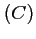 ;
on prendre pou unité 2 cm.
;
on prendre pou unité 2 cm.
- Soit
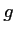 la fonction numérique de la variable réelle
la fonction numérique de la variable réelle 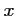 telle
que:
telle
que:
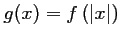 et
et 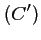 sa courbe représentative.
Sans étudier la fonction
sa courbe représentative.
Sans étudier la fonction 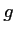 , construire
, construire 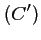 sur le graphique
précédent.
sur le graphique
précédent.
Correction
Tag:Fonctions
Voir aussi:
Quelques devoirs
sur les limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes. Étude, et limites, d'une fonction avec exponentielle
Étude de fonction avec exponentielle et convexité, points d'inflexion, position relative, résolution approchée d'équation à l'aide du TVI
Étude de fonction avec exponentielle et convexité, points d'inflexion, position relative, résolution approchée d'équation à l'aide du TVI - Annales Bac Asie 8 juin 2021 (QCM), 15 mars 2021 et 8 juin 2021
Étude de fonction avec exponentielle et convexité, points d'inflexion, position relative, résolution approchée d'équation à l'aide du TVI - Annales Bac 7 juin 2021 (QCM), 15 mars 2021 et 8 juin 2021
logarithme, seuil pour une suite géométrique, convexité, TVI
