Deux courbes tangentes en un point

On considère les fonctions 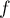et définies respectivement sur 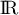et 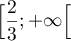par les expressions et .
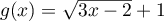On note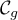 et 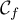leur courbe représentative respective.

1. 1. Déterminer les coordonnées des points d'intersection de et des axes du repère.
   2. Dresser le tableau de variation de 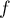. Préciser les limites en l'infini.
2. 1. Etudier la limite de 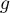en .
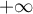   2. Etudier les variations de .
3. 1. Donner l'équation de la tangente à 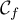au point d'abscisse .
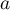   2. On dit que deux courbes sont tangentes en un point lorsque, en ce point, les deux courbes ont la même tangente. Montrer que les courbes 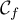et sont tangentes au point d'abscisse .
4. Tracer les courbes 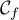et dans un repère en utilisant tous les résultats précédents.

Correction

Autres sujets au hasard: