Bac 2022 (12 mai): Un peu de tout dans l'espace
Exercice corrigé - Spécialité maths, terminale générale
On considère un cube ABCDEFGH
et on appelle K le milieu du segment [BC].
On se place dans le repère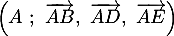 et on considère le tétraèdre EFGK.
et on considère le tétraèdre EFGK.
On rappelle que le volume d'un tétraèdre est donné par:
![\[V=\dfrac13\tm\mathcal{B}\tm h\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/2.png)
où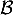 désigne l'aire d'une base et
désigne l'aire d'une base et 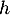 la hauteur relative à cette base.
la hauteur relative à cette base.
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/5.png)
On se place dans le repère
On rappelle que le volume d'un tétraèdre est donné par:
où
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/5.png)
- Préciser les coordonnées des points E, F, G et K.
- Montrer que le vecteur
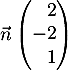 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
- Démontrer que le plan (EGK) admet pour équation cartésienne :
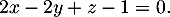
- Déterminer une représentation paramétrique de la droite
 orthogonale au plan (ECK)
passant par F.
orthogonale au plan (ECK)
passant par F.
- Montrer que le projeté orthogonal L de F sur le plan (EGK) a pour coordonnées
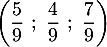 .
.
- Justifier que la longueur LF est égale à
 .
.
- Calculer l'aire du triangle EFG. En déduire que le volume du tétraèdre EFGK est égal à
 .
.
- Déduire des questions précédentes l'aire du triangle EGK.
- On considère les points P milieu du segment [EG], M milieu du segment [EK] et N milieu du segment[GK]. Déterminer le volume du tétraèdre FPMN.
Correction
Cacher la correction
- E( 0 ; 0; 1) ; F( 1 ; 0; 1) ;
G( 1 ; 1 ; 1) ; K( 1 ; 0,5 ; 0)
- On a
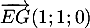 et
et 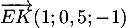 qui sont non colinéaires, et tels que
qui sont non colinéaires, et tels que
![\[\vec{n}\cdot\overrightarrow{EG}=2\tm1+(-2)\tm1+1\tm0=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/3.png)
et
![\[\vec{n}\cdot\overrightarrow{EK}=2\tm1+(-2)\tm0,5+1\tm(-1)=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/4.png)
et donc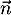 est orthogonal à deux vecteurs colinéaires du plan
(EGK) et donc
est orthogonal à deux vecteurs colinéaires du plan
(EGK) et donc  est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
- On déduit de la question précédente qu'une équation cartésienne du plan (EGK)
s'écrit sous la forme
![\[2x-2y+z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/7.png)
De plus,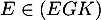 ,
d'où
,
d'où 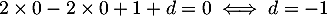 ,
et donc le plan (EGK)
admet bien pour équation cartésienne :
,
et donc le plan (EGK)
admet bien pour équation cartésienne : 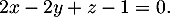
- La droite
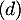 orthogonale au plan (ECK) admet donc
orthogonale au plan (ECK) admet donc 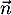 pour vecteur directeur et comme elle passe de plus par F, on peut écrire la représentation paramétrique
pour vecteur directeur et comme elle passe de plus par F, on peut écrire la représentation paramétrique
![\[\la\begin{array}{lclcl}x&=&1&+&2t\\y&=&&-&2t\\z&=&1&+&t\enar\right. \ , \ t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/13.png)
- Comme
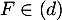 et
et 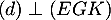 , le projeté orthogonal L de F
sur le plan (EGK) est l'intersection de la droite et du plan.
, le projeté orthogonal L de F
sur le plan (EGK) est l'intersection de la droite et du plan.
En particulier les coordonnées de L vérifient la représentation paramétrique précédente, pour un certain paramètre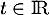 , et aussi l'équation du plan (EGK),
soit
, et aussi l'équation du plan (EGK),
soit
![\[\begin{array}{ll}&2x-2y+z-1=0\\
\iff&2(1+2t)-2(-2t)+(1+t)-1=0\\
\iff&t=-\dfrac29
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/17.png)
d'où les coordonnées de L:
![\[\la\begin{array}{lclclcl}x&=&1&+&2\lp-\dfrac29\rp&=&\dfrac59\\
y&=&&-&2\lp-\dfrac29\rp&=&\dfrac49\\
z&=&1&+&\lp-\dfrac29\rp&=&\dfrac79\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/18.png)
qui sont bien les coordonnées recherchées. -
![\[\begin{array}{ll}LF&=\sqrt{\lp\dfrac59-1\rp^2+\lp\dfrac49-0\rp^2+\lp\dfrac79-1\rp^2}\\[1.4em]
&=\sqrt{\dfrac{4^2+4^2+2^2}{9^2}}
=\sqrt{\dfrac{36}{9^2}}=\sqrt{\dfrac{4}{9}}=\dfrac23
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/19.png)
- Le triangle EFG est isocèle rectangle et a pour aire
![\[\mathcal{A}_{EFG}=\dfrac12EF\times EG=\dfrac12\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/20.png)
Dans le tétraèdre EFGK, la hauteur associée à la base EFG est KK',
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
\psline[linecolor=red,linewidth=1.8pt](4.35,1.05)(4.35,4.55)
\rput(4.2,4.7){K'}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/21.png)
On a KK'=1 et donc le volume
![\[\begin{array}{ll}\mathcal{V}_{EFGK}&=\dfrac13\tm\mathcal{A}_{AEFG}\tm KK'\\[1em]
&=\dfrac13\tm\dfrac12\tm1=\dfrac16\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/22.png)
- On eput aussi calculer ce volume en prenant la base EGK,
la hauteur associée étant alors LF, et on a donc
![\[\begin{array}{ll}&\mathcal{V}_{EFGK}=\dfrac13\tm\mathcal{A}_{EGK}\tm LF\\
\iff& \dfrac16=\dfrac13\tm\mathcal{A}_{EGK}\tm\dfrac23\\
\iff&\mathcal{A}_{EGK}=\dfrac34
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/23.png)
-
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
%
\pspolygon[linecolor=blue](2.6,4.55)(2.275,2.375)(4.675,3.225)%PMN
\psline[linecolor=blue](2.6,4.55)(3.7,3.7)
\psline[linecolor=blue](2.275,2.375)(3.7,3.7)
\psline[linecolor=blue](4.675,3.225)(3.7,3.7)
\rput(2.4,4.7){\blue P}
\rput(2,2.2){\blue M}
\rput(4.84,3.){\blue N}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/24.png)
Comme les deux triangles EGK et PMN sont dans le même plan, les hauteurs qui leurs sont associées dans les deux trétraèdres sont les mêmes, soit LF.
D'arpès le théorème de Thalès, on a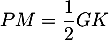 ,
,
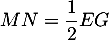 et
et 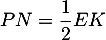 : les longueurs de tous les côtés sont divisées par 2, et l'aire est donc divisée par 4.
: les longueurs de tous les côtés sont divisées par 2, et l'aire est donc divisée par 4.
Finalement, on obtient l'aire du tétraèdre:
![\[\begin{array}{ll}
\mathcal{V}_{FPMN}&=\dfrac13\tm\mathcal{A}_{PMN}\tm LF\\
&=\dfrac13\tm\lp\dfrac14\tm\dfrac34\rp\tm\dfrac23\\
&=\dfrac1{24}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/28.png)
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
