Bac 2021 (sujet 1): Suite récurrente
Exercice corrigé - Spécialité maths, terminale générale
La suite 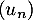 est définie sur
est définie sur 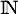 par
par 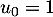 et pour tout entier naturel
et pour tout entier naturel  ,
,
![\[u_{n+1} = \dfrac34u_n + \dfrac14n + 1.\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021/5.png)
- Calculer, en détaillant les calculs,
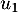 et
et 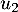 sous forme de fraction irréductible.
sous forme de fraction irréductible.
L'extrait, reproduit ci-contre, d'une feuille de calcul réalisée avec un tableur présente les valeurs des premiers termes de la suite 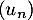 .
.
![\[\begin{tabular}{|c|*2{p{2.4cm}|}}\hline
& A&B \\ \hline
1 &$n$&$u_n$\\ \hline
2 &0 &1\\ \hline
3 &1 &1,75\\ \hline
4 &2 &2,5625\\ \hline
5 &3 &3,421875\\ \hline
6 &4 &4,31640625\\ \hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021/9.png)
-
- Quelle formule, étirée ensuite vers le bas, peut-on écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
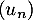 dans la colonne B ?
dans la colonne B ?
- Conjecturer le sens de variation de la suite
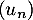 .
.
- Quelle formule, étirée ensuite vers le bas, peut-on écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
-
- Démontrer par récurrence que, pour tout entier naturel
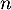 , on a :
, on a : 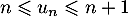 .
.
- En déduire, en justifiant la réponse, le sens de variation et la limite de la suite
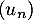 .
.
- Démontrer que :
![\[\lim_{n \to + \infty} \dfrac{u_n}n = 1\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021/15.png)
- Démontrer par récurrence que, pour tout entier naturel
- On désigne par
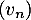 la suite définie sur
la suite définie sur  par
par 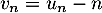
- Démontrer que la suite
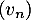 est géométrique
de raison
est géométrique
de raison  .
.
- En déduire que, pour tout entier naturel
 ,on a:
,on a:
 .
.
- Démontrer que la suite
Correction
Cacher la correction
- Pour
 ,
, 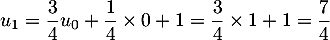 .
.
Pour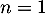 ,
, 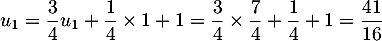 .
.
-
- La formule, étirée ensuite vers le bas, que l'on peut écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
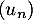 dans la colonne B est:
= 3/4 * B2 + 1/4 * A2 +1
dans la colonne B est:
= 3/4 * B2 + 1/4 * A2 +1
- La suite
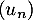 semble croissante.
semble croissante.
- La formule, étirée ensuite vers le bas, que l'on peut écrire dans la cellule B3 de la feuille de calcul pour obtenir les termes successifs de
-
- Soit
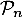 la propriété:
la propriété: 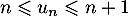 .
.
Initialisation
Pour ,
, 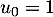 et
et 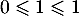 donc
donc 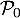 est vraie.
est vraie.
Hérédité
Supposons que, pour un certain entier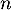 ,
, 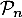 est vraie,
c'est-à-dire:
est vraie,
c'est-à-dire: 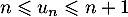 .
.
Alors,
![\[\begin{array}{ll}&n\leqslant u_n \leqslant n+1\\[.6em]
\iff&\dfrac34n\leqslant\dfrac34u_n\leqslant\dfrac34(n+1)\\[.8em]
\iff&\dfrac34n +\dfrac14n\leqslant\dfrac34u_n+\dfrac14n\leqslant\dfrac34(n+1)+\dfrac14n\\[.6em]
\iff&n \leqslant\dfrac34u_n+\dfrac14n \leqslant n+\dfrac34\\[7pt]
\iff&n+1 \leqslant\dfrac34u_n+\dfrac14n+1\leqslant n+\dfrac34+1\\
\iff&n+1 \leqslant u_{n+1}\leqslant n+\dfrac74\leqslant n+2\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/16.png)
ce qui montre que la propriété est encore vraie au rang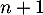 .
.
Conclusion On vient donc de démonter, d'après le principe de récurrence, que, pour tout entier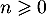 ,
,
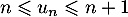 .
.
-
D'après la question précédente, pour tout
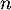 ,
, 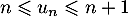 donc aussi, au rang suivant,
donc aussi, au rang suivant, 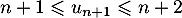 .
.
On a alors,
![\[n \leqslant u_n \leqslant n+1 \leqslant u_{n+1} \leqslant n+2\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/23.png)
et donc, entre autre que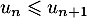 , c'est-à-dire que la suite
, c'est-à-dire que la suite 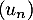 est croissante.
est croissante.
On a aussi de ces inégalités que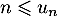 ,
et comme
,
et comme 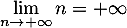 donc, par comparaison
(corollaire du théorème des gendarmes),
donc, par comparaison
(corollaire du théorème des gendarmes),
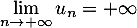 .
.
- Pour tout
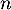 ,
, 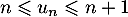 donc on a aussi
donc on a aussi
![\[1 \leqslant \dfrac{u_n}{n} \leqslant \dfrac{n+1}{n}=1+\dfrac{1}{n}\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/31.png)
avec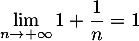 ,
donc, d'après le théorème des gendarmes:
,
donc, d'après le théorème des gendarmes: 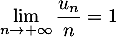 .
.
- Soit
- On désigne par
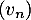 la suite définie sur
la suite définie sur 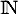 par
par 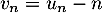
- Pour tout
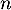 ,
, 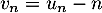
![\[\begin{array}{ll}v_{n+1}&=u_{n+1} - (n+1) \\[.4em]
&=\dfrac34u_n + \dfrac{1}{4}n+1 -n-1\\[.7em]
&=\dfrac34u_n -\dfrac34n\\[.7em]
&=\dfrac34\left( u_n -n\rp\\[.7em]
&=\dfrac{3}{4}v_n\enar\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/39.png)
Donc la suite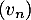 est géométrique de raison
est géométrique de raison 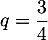 et de premier terme
et de premier terme 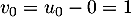
- On en déduit que, pour tout
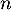 ,
,
![\[v_n=v_0\times q^n = \lp\dfrac34\rp^n\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/44.png)
et donc aussi que
![\[u_n=v_n+n=\lp\dfrac34\rp^n+n\]](/Generateur-Devoirs/TS/ChapSuites/ex15032021_c/45.png)
- Pour tout
Cacher la correction
Tag:Suites
Voir aussi:
