Bac 2021 (sujet 0): Logarithme et convexité
Exercice corrigé - Spécialité maths, terminale générale
Sur le graphique ci-dessous, on a représenté dans un repère orthonormé :
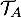 est parallèle à l’axe des abscisses. La droite
est parallèle à l’axe des abscisses. La droite 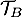 coupe l’axe des abscisses au point de coordonnées (3 ; 0) et l’axe des ordonnées au point de coordonnées (0 ; 3).
coupe l’axe des abscisses au point de coordonnées (3 ; 0) et l’axe des ordonnées au point de coordonnées (0 ; 3).
(\n,3.5)}
%\multido{\n=0+1}{51}{\psline[linewidth=0.3pt](\n,-100)(\n,100)}
\multido{\n=-0.5+0.5}{8}{\psline[linewidth=0.35pt,linecolor=lightgray](0,\n)(7.50,\n) }
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5]{->}(0,0)(0,-0.5)(7.6,3.6)
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5](0,0)(0,-0.5)(7.6,3.6)
\psplot[linewidth=1.25pt,linecolor=blue,plotpoints=5000]{0.127}{7.50}{x ln 2 add x div}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{7.50}{2.71828}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{3.50}{x neg 3 add}
\psdots[dotstyle=Bullet,dotscale =1.1](0.367879,2.71828)(1,2)
\uput[ur](0.468,2.81828){A}\uput[ur](1.1,2.1){B}
\uput[u](6.5,2.5){\cyan $\mathcal{T}_A$}
\uput[r](2.2,0.5){\cyan $\mathcal{T}_B$}
\uput[r](5,0.5) {\blue $\mathcal{C}_f$}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/11.png)
On note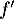 la fonction dérivée de
la fonction dérivée de 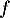 .
.
Partie I
Partie II
On suppose maintenant que la fonction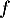 est définie sur
est définie sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/18.png) par :
par :
![\[f(x) =\dfrac{2+\ln(x)}{x}.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/19.png)
- la courbe représentative
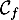 d’une fonction
d’une fonction 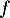 définie et dérivable sur
définie et dérivable sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/3.png) ;
;
- la tangente
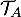 à la courbe
à la courbe 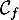 au point A de coordonnées
au point A de coordonnées 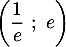 ;
;
- la tangente
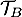 à la courbe
à la courbe 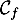 au point B de coordonnées (1 ; 2).
au point B de coordonnées (1 ; 2).
(\n,3.5)}
%\multido{\n=0+1}{51}{\psline[linewidth=0.3pt](\n,-100)(\n,100)}
\multido{\n=-0.5+0.5}{8}{\psline[linewidth=0.35pt,linecolor=lightgray](0,\n)(7.50,\n) }
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5]{->}(0,0)(0,-0.5)(7.6,3.6)
\psaxes[linewidth=0.95pt,Dx=0.5,Dy=0.5](0,0)(0,-0.5)(7.6,3.6)
\psplot[linewidth=1.25pt,linecolor=blue,plotpoints=5000]{0.127}{7.50}{x ln 2 add x div}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{7.50}{2.71828}
\psplot[linewidth=0.85pt,linecolor=cyan,plotpoints=5000]{-0.1}{3.50}{x neg 3 add}
\psdots[dotstyle=Bullet,dotscale =1.1](0.367879,2.71828)(1,2)
\uput[ur](0.468,2.81828){A}\uput[ur](1.1,2.1){B}
\uput[u](6.5,2.5){\cyan $\mathcal{T}_A$}
\uput[r](2.2,0.5){\cyan $\mathcal{T}_B$}
\uput[r](5,0.5) {\blue $\mathcal{C}_f$}
$$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/11.png)
On note
Partie I
- Déterminer graphiquement les valeurs de
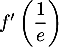 et de
et de 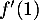 .
.
- En déduire une équation de la droite
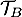 .
.
Partie II
On suppose maintenant que la fonction
- Par le calcul, montrer que la courbe
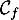 passe par les points A et B et qu’elle coupe l’axe des abscisses en un point unique que l’on précisera.
passe par les points A et B et qu’elle coupe l’axe des abscisses en un point unique que l’on précisera.
- Déterminer la limite de
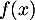 quand
quand 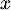 tend vers 0 par valeurs supérieures, et la limite de
tend vers 0 par valeurs supérieures, et la limite de 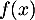 quand
quand 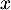 tend vers
tend vers 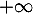 .
.
- Montrer que, pour tout
![$x\in]0~;~\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/26.png) ,
,
![\[f'(x)=\dfrac{-1-\ln(x)}{x^2} .\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/27.png)
- Dresser le tableau de variations de
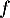 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/29.png) .
.
- On note
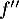 la fonction dérivée seconde de
la fonction dérivée seconde de 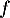 On admet que, pour tout
On admet que, pour tout ![$x\in]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/32.png)
![\[f''(x)=\dfrac{1+2\ln(x)}{x^3} .\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0/33.png)
Déterminer le plus grand intervalle sur lequel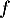 est convexe.
est convexe.
Correction
Partie I
Partie II
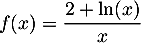 ,
pour
,
pour 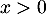
Cacher la correction
Partie I
-
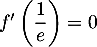 car c'est le coefficient directeur de la tangente
car c'est le coefficient directeur de la tangente
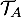 , qui est horizontale.
, qui est horizontale.
De même,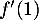 est le coefficient directeur de la tangente
est le coefficient directeur de la tangente
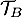 , qui passe par le point
, qui passe par le point 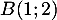 et le point
de l'axe des abscisses de coordonnées
et le point
de l'axe des abscisses de coordonnées 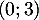 .
.
Ce coefficient directeur est donc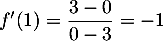 .
.
- La droite
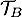 a pour coefficient directeur
a pour coefficient directeur 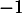 et 3 pour ordonnée à l'origine, donc elle a pour équation:
et 3 pour ordonnée à l'origine, donc elle a pour équation: 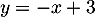 .
.
Partie II
-
-
![\[f\lp\dfrac1e\right) = \dfrac{2+\ln\lp\frac1e\right)}{\frac1e}
= e\left( 2 - \ln(e)\right) = e( 2 - 1)=e\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/13.png)
donc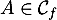 .
.
-
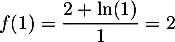 donc
donc 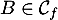 .
.
- La courbe
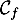 coupe l'axe des abscisses en un point dont l'abscisse est solution de l'équation
coupe l'axe des abscisses en un point dont l'abscisse est solution de l'équation 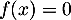 , soit,
, soit,
![\[\begin{array}{ll}f(x)=0
&\iff \dfrac{2+\ln(x)}{x} = 0\\
&\iff 2+\ln(x)=0\\
&\iff \ln(x)=-2\\
&\iff x = e^{-2}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/19.png)
Donc la courbe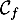 coupe l'axe des abscisses en un point unique de coordonnées
coupe l'axe des abscisses en un point unique de coordonnées 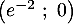 .
.
-
-
On a
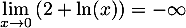 et
et 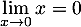 , avec
, avec 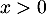 , d'où, par quotient des limites,
, d'où, par quotient des limites,
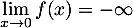 .
.
On a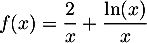 ,
avec
,
avec
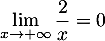 et, par croissances comparées,
et, par croissances comparées,
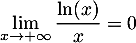
d'où,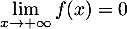 .
.
- Pour
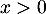 , en dérivant le quotient
, en dérivant le quotient 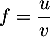 , on a
, on a
![\[\begin{array}{ll}f'(x)&=\dfrac{\frac1x\times x - (2+\ln(x)) \times1}{x^2} \\[.8em]
&= \dfrac{1-2-\ln(x)}{x^2} = \dfrac{-1-\ln(x)}{x^2}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/32.png)
- On a
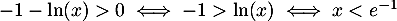
On dresse le tableau de variations de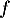 sur
sur ![$]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/35.png) :
:
![\[\renewcommand{\arraystretch}{1.3}
\psset{nodesep=3pt,arrowsize=2pt 3}% param\`etres
\def\esp{\hspace*{2.5cm}}% pour modifier la largeur du tableau
\def\hauteur{0pt}% mettre au moins 20pt pour augmenter la hauteur
\begin{array}{|c|l *4{c}|}
\hline
x & 0 & \esp & e^{-1} & \esp & +\infty \\
\hline
-1-\ln(x)&\vline\;\vline & + & \vline\hspace{-2.7pt}0 & - & \\ \hline
x^2 &0 && + & & \\\hline
f'(x) &\vline\;\vline & \pmb{+} & \vline\hspace{-2.7pt}0 & \pmb{-} & \\
\hline
& \vline\;\vline & & \Rnode{max}{e} & & \\
f(x) &\vline\;\vline & & & & \rule{0pt}{\hauteur} \\
& \vline\;\vline \Rnode{min1}{~-\infty} & & & & \Rnode{min2}{0} \rule{0pt}{\hauteur}
\ncline{->}{min1}{max}
\ncline{->}{max}{min2}
\\
\hline\end{array}\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/36.png)
- La fonction
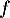 est convexe lorsque
est convexe lorsque 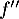 est positive,
soit
est positive,
soit
![\[\begin{array}{ll}f''(x)\geqslant 0
&\iff \dfrac{1+2\ln(x)}{x^3} \geqslant 0\\[.8em]
&\iff 1+2\ln(x) \geqslant 0\\[.6em]
&\iff \ln(x) \geqslant -\dfrac12\\
&\iff x\geqslant e^{-\frac{1}{2}}
\enar\]](/Generateur-Devoirs/TS/ChapLogarithme/ex2021-sujet-0_c/39.png)
Donc le plus grand intervalle sur lequel la fonction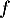 est convexe est
est convexe est 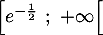 .
.
Cacher la correction
Tags:LogarithmeConvexité
Voir aussi:
