Exercice corrigé bac S juin 2015 - Analyse: logarithme, algorithme et intégrale
Pentes dans un skateparc, et surface à peindre
Exercice corrigé de mathématiques: Exercice corrigé Bac S juin 2015: Etudes de fonctions avec un logarithme, calculs de pentes, tangentes, et intégrales
Exercice - énoncé:
![\psset{unit=0.3cm}
\begin{pspicture}(-1.5,-1.5)(29,19)
\psaxes[linewidth=1.pt,labels=none,tickstyle=bottom]{->}(0,0)(29,19)
\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}
\rput(7.07,7.07){\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}}
\pspolygon[showpoints](20,0)(27.07,7.07)(27.07,18.005)(20,10.935)%DD'C'C
\psline[showpoints](0,7.07)(7.07,14.14)%BB'
\psline[showpoints,linestyle=dashed](0,0)(7.07,7.07)(27.07,7.07)
\psline[linestyle=dashed,showpoints](7.07,7.07)(7.07,14.14)
\uput[dl](0,0){O} \uput[ul](7.07,7.07){A} \uput[l](0,7.07){B}
\uput[ul](7.07,14.14){B$'$} \uput[dr](20,10.935){C} \uput[dr](27.07,18.005){C$'$}
\uput[d](20,0){D} \uput[dr](27.07,7.07){D$'$} \uput[d](1,0){I}
\uput[l](0,1){J}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/1.png) |
Une municipalité a décidé d'installer un module de skateboard dans un parc de la commune.
Le dessin ci-contre en fournit une perspective cavalière. Les quadrilatères Le plan de face L'unité est le mètre. La largeur du module est de 10 mètres, autrement dit, |
Le but du problème est de déterminer l'aire des différentes surfaces à peindre.
Le profil du module de skateboard a été modélisé à partir d'une photo par la fonction
On note
Partie 1
|
![\psset{unit=0.3cm}
\begin{pspicture}(-1.5,-1.5)(23,13.5)
\psaxes[linewidth=1.25pt,labels=none,tickstyle=bottom]{->}(0,0)(23,13.5)
\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}
\uput[u](15,7){$\mathcal{C}$}\uput[d](20,0){D}\uput[l](0,7.07){B}\uput[dr](20,10.935){C}\uput[dl](0,0){O}\uput[d](1,0){I}
\uput[l](0,1){J}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/23.png) |
4. On admet que la fonction
a pour dérivée la fonction
Déterminer une primitive de la fonction
Partie 2
Les trois questions de cette partie sont indépendantes
- Les propositions suivantes sont-elles exactes ? Justifier les réponses.
- [
 :] La différence de hauteur entre le point le plus haut et le point le plus bas de la piste est au moins égale à 8 mètres.
:] La différence de hauteur entre le point le plus haut et le point le plus bas de la piste est au moins égale à 8 mètres.
- [
 :] L'inclinaison de la piste est presque deux fois plus grande en
:] L'inclinaison de la piste est presque deux fois plus grande en  qu'en
qu'en  .
.
- [
- On souhaite recouvrir les quatre faces latérales de ce module d'une couche de peinture rouge. La peinture utilisée permet de couvrir une surface de
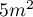 par litre.
par litre.
Déterminer, à 1 litre près, le nombre minimum de litres de peinture nécessaires.
-
On souhaite peindre en noir la piste roulante, autrement dit la surface supérieure du module.
Afin de déterminer une valeur approchée de l'aire de la partie à peindre, on considère dans le repère (O, I, J) du plan de face, les points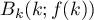 pour
pour  variant de 0 à 20.
variant de 0 à 20.
Ainsi,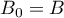 .
.
On décide d'approcher l'arc de la courbe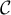 allant de
allant de 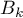 à
à 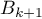 par le segment
par le segment ![$\left[B_kB_{k+1}\right]](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/43.png) .
.
Ainsi l'aire de la surface à peindre sera approchée par la somme des aires des rectangles du type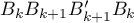 (voir figure).
(voir figure).
![\psset{xunit=0.3cm,yunit=0.35cm}
\begin{pspicture}(-2.2,-1.5)(29,17)
\psaxes[linewidth=1.25pt,labels=none,tickstyle=bottom]{->}(0,0)(29,19)
\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}
\rput(7.07,7.07){\psplot[plotpoints=5000,linewidth=1.25pt]{0}{20}{x 1 add ln x 1 add mul 3 x mul sub 7 add}}
\pspolygon(20,0)(27.07,7.07)(27.07,18.005)(20,10.935)%DD'C'C
\psline(0,7.07)(7.07,14.14)%BB'
\psline[linestyle=dashed](0,0)(7.07,7.07)(27.07,7.07)
\psline[linestyle=dashed](7.07,7.07)(7.07,14.14)
\uput[dl](0,0){O} \uput[ul](7.07,7.07){\scriptsize A} \uput[l](0,7.07){\scriptsize B}
\uput[ul](7.07,14.14){\scriptsize B$'$} \uput[dr](20,10.935){\footnotesize C} \uput[dr](27.07,18.005){\footnotesize C$'$}
\uput[d](20,0){\scriptsize D} \uput[dr](27.07,7.07){\scriptsize D$'$} \uput[d](1,0){\scriptsize I}
\psline[linestyle=dotted](1,5.39)(8.07,12.46)\uput[d](1,5.48){\scriptsize $B_1$}\uput[ur](8.07,12.46){\footnotesize $B'_1$}
\psline[linestyle=dotted](2,4.3)(9.07,11.37) \uput[d](2,4.34){\scriptsize $B_2$}\uput[ur](9.07,11.37){\footnotesize $B'_2$}
\psline[linestyle=dotted](7,2.64)(14.07,9.71)\uput[dl](7,2.64){\scriptsize $B_k$}\uput[ul](14.07,9.71){\footnotesize $B'_k$}
\psline[linestyle=dotted](8,2.78)(15.07,9.85)\uput[d](9,3.03){\scriptsize $B_{k+1}$}\uput[u](16.07,10.1){\scriptsize $B'_{k+1}$}
\uput[l](0,1){J}
\end{pspicture}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin/45.png)
- Montrer que pour tout entier
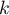 variant de 0 à 19,
variant de 0 à 19,
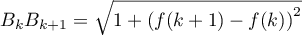 .
.
- Compléter l'algorithme suivant pour qu'il affiche une estimation de l'aire de la partie roulante.
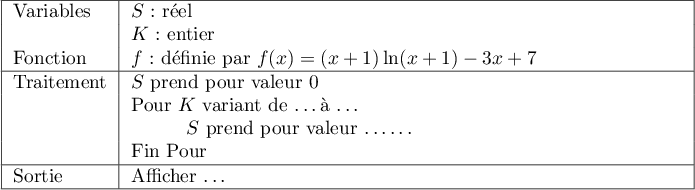
- Montrer que pour tout entier
Correction exercice
Partie 1
-
 avec
avec 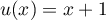 , donc
, donc 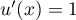 ,
,
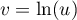 , donc
, donc  soit
soit 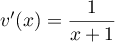 et
et 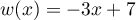 donc
donc 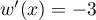 .
.
On a alors ,
soit
,
soit 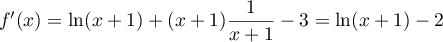 .
.
-
 , par croissance de la
fonction exponentielle, et donc
, par croissance de la
fonction exponentielle, et donc  .
.
![\begin{tabular}{|c|ccccc|}\hline
x&0&&$e^{2}-1$&&20\\\hline
$f'(x)$&&-&\zb&+&\\\hline
&7&&&&$f(20)\simeq 10,93$\\
$f(x)$&&\psline[arrowsize=7pt]{->}(-.4,.4)(.6,-.5)&&
\psline[arrowsize=7pt]{->}(-.6,-.5)(.4,.4)&\\
&&&$\begin{array}{c}f\left( e^{2}-1\rp\\=10-e^2\simeq 2,6\enar$&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapIntegration/ex2015-Metropole-juin_c/13.png)
- Le coefficient directeur de la tangente à
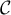 au point d'abscisse
au point d'abscisse 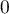 est
est  .
.
- Une primitive de
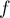 est donc donnée par
est donc donnée par
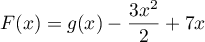
Partie 2
-
- La différence entre les points le plus haut et le plus bas est
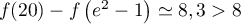 donc
donc 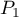 est vraie.
est vraie.
-
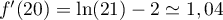 . D'après la question 3.,
l'inclinaison en
. D'après la question 3.,
l'inclinaison en  est 2, donc
est 2, donc  est vraie.
est vraie.
- La différence entre les points le plus haut et le plus bas est
- L'aire de la face avant, en unités d'aire, vaut
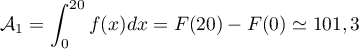 .
.
L'aire latérale gauche vaut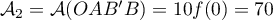 .
.
L'aire latérale droite vaut .
.
L'aire à peindre est donc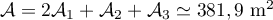 .
.
Il faut prévoir donc au minimum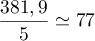 litres de peinture.
litres de peinture.
-
-
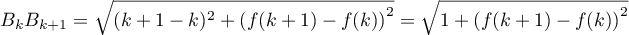 .
.
- La partie de l'algorithme à compléter est :
 prend la valeur 0.
prend la valeur 0.
Pour allant de 0 à 19
allant de 0 à 19
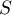 prend la valeur
prend la valeur 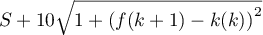
Fin Pour
-
Cacher la correction
Voir aussi: