Exercice (type) bac - Probabilités: intervalle de fluctuation

Crise d'asthme chez les enfants



Exercice corrigé de mathématiques: Exercice corrigé - Probabilités: intervalle de fluctuation du nombre de crises d'asthme chez les enfants

Exercice - énoncé:

On admet que, en France, dans la population d'enfants de 11 à 14 ans, le pourcentage d'enfants ayant déjà eu une crise d'asthme dans leur vie est de 13 %.
Un médecin d'une ville est surpris du nombre important d'enfants le consultant ayant des crises d'asthme et en informe les services sanitaires. Ceux-ci décident d'entreprendre une étude et d'évaluer la proportion d'enfants de 11 à 14 ans ayant déjà eu des crises d'asthme. Ils selectionnent de manière aléatoire 100 jeunes de 11 à 14 ans de la ville.
  1. Déterminer l'intervalle de fluctuation asymptotique au seuil de 95 % de la proportion de jeunes de 11 à 14 ans ayant déjà eu une crise d'asthme dans un échantillon de 100 enfants.
  2. L'étude réalisée auprès de ces 100 jeunes a dénombré 19 jeunes ayant déjà eu des crises d'asthme.
    Que peut-on en conclure ?
  3. Le médecin n'est pas convaincu par cette conclusion et déclare que le nombre de jeunes interrogés était insuffisant pour mettre en évidence qu'il y avait plus de jeunes ayant des crises d'asthme que dans le reste de la France.
    Combien faudrait-il prendre de sujets pour qu'une proportion observée de 19 % soit en dehors de l'intervalle de fluctuation asymptotique ?

Correction exercice


  1. L'intervalle de fluctation au seuil de 95 % d'une proportion sur un échantillon de 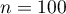jeunes est:

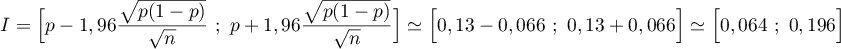
  2. Lors de cette étude, de jeunes ont déjà eu une crise d'asthme. Comme , on ne peut pas conclure au fait que le nombre de jeunes ayant déjà eu une crise d'asthme dans cette ville soit particulièrement important; ce nombre qui paraît important pour le médecin peut s'expliquer par la fluctuation aléatoire d'un échantillon à l'autre de 100 jeunes.
  3. Il faut que .
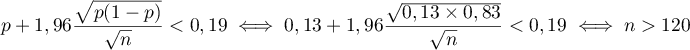    La taille de l'échantillon de jeunes interrogés doit donc être de 121 jeunes au minimum si on souhaite mettre en évidence une proportion anormalement élevée dans cette ville.


Cacher la correction


Voir aussi:
ccc