Exercice (type) bac - Probabilités: lois binomiales, normales et intervalle de confiance
Production de plaques métalliques
Exercice corrigé de mathématiques: Exercice corrigé - Production de plaques métalliques (lois binomiale, normale et intervalle de confiance)
Exercice - énoncé:
Une entreprise produit en grande série des plaques métalliques
rectangulaires pour l'industrie automobile.
Dans ce qui suit, les résultats approchés seront arrondis au
centième.
Partie A. On note
l'événement "une plaque prélevée au hasard dans la
production d'une journée est défectueuse".
On suppose que 
.
On prélève au hasard 50 plaques dans la production de la journée pour vérification. La production est assez importante pour que l'on puisse assimiler ce prélévement à un tirage aléatoire avec remise de 50 plaques.
On considère la variable aléatoire
qui, à tout prélévement ainsi
défini, associe le nombre de plaques de ce prélévement qui sont
défectueuses.
Partie B. Une plaque de ce type a une longueur conforme lorsque sa longueur
,
exprimée en millimètres, appartient à l'intervalle 
.
Une plaque de ce type a une largeur conforme lorsque sa largeur
,
exprimée en millimètres, appartient à l'intervalle 
.
Partie C. Dans cette partie, on considère une grande quantité de plaques destinée à une chaîne de montage de véhicules électriques. On considère un échantillon de 100 plaques prélevées au hasard dans cette livraison. La livraison est assez importante pour que l'on puisse assimiler ce tirage à un tirage aléatoire avec remise.
On constate que 94 plaques sont sans défaut.
Partie A.
Partie B.
Partie C.
Partie A. On note
l'événement "une plaque prélevée au hasard dans la
production d'une journée est défectueuse".
On suppose que .
On prélève au hasard 50 plaques dans la production de la journée pour vérification. La production est assez importante pour que l'on puisse assimiler ce prélévement à un tirage aléatoire avec remise de 50 plaques.
On considère la variable aléatoire
qui, à tout prélévement ainsi
défini, associe le nombre de plaques de ce prélévement qui sont
défectueuses.
- Justifier que la variable
suit une loi binomiale dont on
déterminera les paramètres.
- Calculer les probabilités
et 
.
- Calculer la probabilité que, dans un prélévement, au plus deux plaques soient défectueuses.
Partie B. Une plaque de ce type a une longueur conforme lorsque sa longueur
,
exprimée en millimètres, appartient à l'intervalle .
Une plaque de ce type a une largeur conforme lorsque sa largeur
,
exprimée en millimètres, appartient à l'intervalle .
- On note
la variable aléatoire qui, à chaque plaque de ce
type prélevée au hasard dans un stock important, associe sa longueur
.
On suppose que la variable aléatoire 
suit la loi normale de
moyenne 550 et d'écart-type 1.
Calculer
.
- On note
la variable aléatoire qui, à chaque plaque de ce
type prélevée au hasard dans un stock important, associe sa largeur
.
On admet que
.
On suppose que les événements "la plaque a une largeur conforme" et "la plaque a une longueur conforme" sont indépendants.
On prélève une plaque au hasard dans le stock.
Déterminer la probabilité que sa largeur et sa longueur soient conformes.
Partie C. Dans cette partie, on considère une grande quantité de plaques destinée à une chaîne de montage de véhicules électriques. On considère un échantillon de 100 plaques prélevées au hasard dans cette livraison. La livraison est assez importante pour que l'on puisse assimiler ce tirage à un tirage aléatoire avec remise.
On constate que 94 plaques sont sans défaut.
- Quelle est la proportion
de plaques sans défaut dans cet
échantillon ?
- A partir de cet échantillon, déterminer un intervalle de
confiance de la proportion
des plaques sans défaut dans la
livraison, au niveau de confiance de 0,95.
- Quelle devrait être la taille de l'échantillon pour que l'intervalle de confiance ait une amplitude inférieure ou égale à 10 % ?
Correction exercice
Partie A.
- On répète
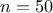fois l'expérience: prélever au hasard une
plaque, dont le succès est l'évenement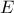 
de probabilité
.
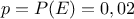Ces répétitions sont identiques et indépendantes (car on assimile
chaque tirage comme étant avec remise).
La variable aléatoire
compte le nombre de succès sur les 50
répétitions, c'est-à-dire le nombre de plaques défectueuses.
Ainsi,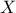
suit la loi binomiale 
.
-
;
.
- La probabilité que, dans un prélévement, au plus deux
plaques soient défectueuses est:
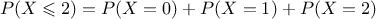
Il ne reste plus qu'à calculer
,
et alors,
.
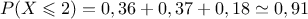Partie B.
- La variable aléatoire
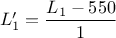suit la loi
normale centrée réduite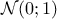 
, pour laquelle on peut
alors utiliser les valeurs de la fonction de répartition 
tabulées:
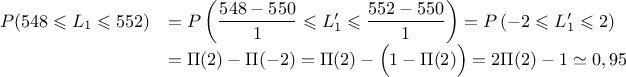
Remarque: On cherche en fait la probabilité d'être à moins de 2 écart-types de la moyenne; on sait alors que pour une loi normale, cette probabilité est d'environ 95 %=0,95, valeur qu'on retrouve ici.
- La probabilité que sa largeur et sa longueur soient
conformes est:
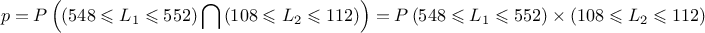
car ces deux événements sont supposés indépendants, et donc,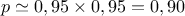
.
Partie C.
- La proportion de plaques sans défaut dans cet
échantillon est
.
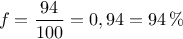- A partir de cet échantillon, un intervalle de
confiance de la proportion
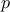des plaques sans défaut dans la
livraison, au niveau de confiance de 0,95, est:
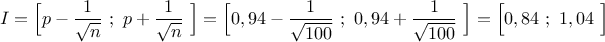
L'intervalle de confiance est donc, au niveau de confiance de 0,95,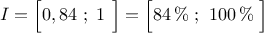
.
- L'amplitude de l'intervalle de confiance est
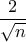, on doit donc avoir une taille 
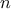de
l'échantillon telle que
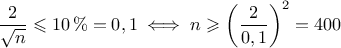
Cacher la correction
Voir aussi: