Exercice corrigé bac S juin 2014- Nombres complexes: Equation bicarrée
Equation bicarrée complexe
Exercice corrigé de mathématiques: Exercice corrigé Bac S, métropole juin 2014: Equation bicarrée complexe
Exercice - énoncé:
On désigne par (E) l'équation
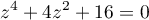
d'inconnue complexe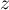 .
.
Cacher la correction
d'inconnue complexe
- Résoudre dans
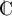 l'équation
l'équation 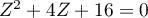 .
.
Écrire les solutions de cette équation sous une forme exponentielle. - On désigne par
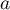 le nombre complexe dont le module est égal à
2 et dont un argument est égal à
le nombre complexe dont le module est égal à
2 et dont un argument est égal à 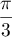 .
.
Calculer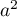 sous forme algébrique.
sous forme algébrique.
En déduire les solutions dans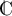 de l'équation
de l'équation
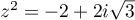 .
On écrira les solutions sous forme algébrique.
.
On écrira les solutions sous forme algébrique.
- Restitution organisée de connaissances
On suppose connu le fait que pour tout nombre complexe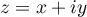 où
où 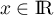 et
et 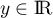 ,
le conjugué de
,
le conjugué de 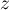 est le nombre complexe
est le nombre complexe
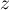 défini par
défini par 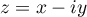 .
.
Démontrer que:
- Pour tous nombres complexes
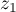 et
et
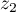 ,
, 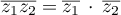 .
.
- Pour tout nombre complexe
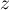 et tout entier naturel non nul
et tout entier naturel non nul 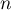 ,
,
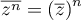 .
.
- Pour tous nombres complexes
- Démontrer que si
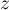 est une solution de l'équation (E) alors
son conjugué
est une solution de l'équation (E) alors
son conjugué 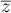 est également une solution de (E).
est également une solution de (E).
En déduire les solutions dans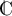 de l'équation (E).
On admettra que (E) admet au plus quatre solutions.
de l'équation (E).
On admettra que (E) admet au plus quatre solutions.
Correction exercice
- Le discriminant
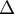 de ce trinôme du second degré est:
de ce trinôme du second degré est:
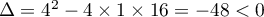 .
L'équation admet donc deux solutions complexes conjuguées, qui sont:
.
L'équation admet donc deux solutions complexes conjuguées, qui sont:
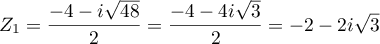 et
et 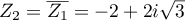 .
.
On a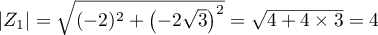 .
On peut alors écrire:
.
On peut alors écrire:
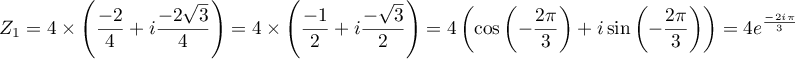
et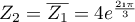 .
.
-
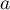 a pour module 2 et pour argument
a pour module 2 et pour argument 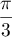 ,
alors
,
alors 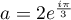 et donc, d'après les propriété du module et des arguments,
et donc, d'après les propriété du module et des arguments,
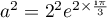 ,
donc
,
donc 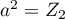 et la forme algébrique de
et la forme algébrique de 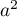 est
est 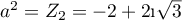 .
Le nombre
.
Le nombre 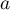 est donc une solution à l'équation dont on parle dans
cette question.
L'autre solution sera donc
est donc une solution à l'équation dont on parle dans
cette question.
L'autre solution sera donc 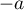 , car
, car 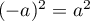 .
.
Sous forme algébrique: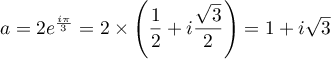 et
et 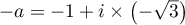 .
.
- Soient
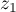 et
et 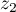 deux nombres complexes.
Il existe donc quatre nombres réels
deux nombres complexes.
Il existe donc quatre nombres réels 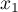 ;
; 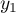 ;
; 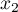 et
et 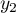 tels que
tels que 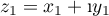 et
et 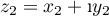 .
.
On a alors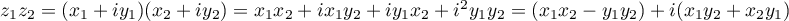
Comme les nombres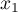 ,
, 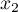 ,
, 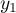 et
et 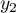 sont réels, alors on
peut définir les nombres
sont réels, alors on
peut définir les nombres 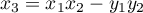 et
et 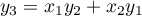 , qui sont réels également.
, qui sont réels également.
On a donc écrit le produit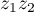 sous la forme
sous la forme 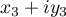 ,
où
,
où 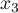 et
et 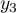 sont des nombres réels, donc le conjugué de
sont des nombres réels, donc le conjugué de
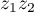 est:
est:
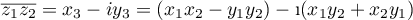 .
.
Par ailleurs,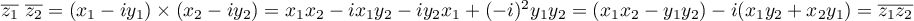
Nous avons donc démontré que pour deux nombres complexes quelconques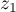 et
et 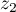 , on a :
, on a : 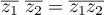 .
.
Initialisation: Pour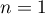 , on a
, on a 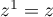 ,
donc
,
donc 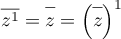 et la propriété est donc vraie au rang
et la propriété est donc vraie au rang 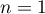 .
.
Hérédité: Supposons la propriété vraie pour un certain entier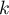 non nul, c'est-à-dire que l'on suppose que pour tout complexe
non nul, c'est-à-dire que l'on suppose que pour tout complexe
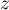 , on a
, on a 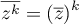 .
.
Soit alors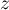 un nombre complexe quelconque.
On a
un nombre complexe quelconque.
On a 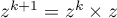 , donc
, donc
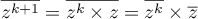 , d'après la première propriété
démontrée, d'où
, d'après la première propriété
démontrée, d'où
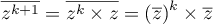 par hypothèse de récurrence.
par hypothèse de récurrence.
Ainsi donc,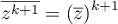 , ce qui montre que la
propriété est encore vraie au rang suivant
, ce qui montre que la
propriété est encore vraie au rang suivant 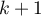 .
.
Conclusion: La propriété est vraie au rang 1 et est héréditaire, donc, d'après le principe de récurrence, pour tout entier naturel non nul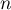 , et pour tout nombre complexe
, et pour tout nombre complexe
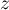 ,
,
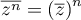 .
.
- Soit
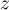 une solution de l'équation
une solution de l'équation 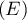 ,
c'est-à-dire que:
,
c'est-à-dire que: 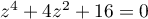 .
.
Soit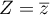 le conjuqué de
le conjuqué de 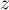 , alors d'après les
propriétés précédentes
, alors d'après les
propriétés précédentes
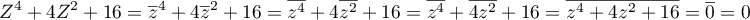
Ainsi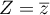 est aussi solution de
est aussi solution de 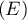 .
.
Comme on a établi à la question 2. que les nombres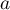 et
et 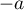 sont
tels que
sont
tels que 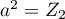 et
et 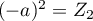 ,
c'est-à-dire que
,
c'est-à-dire que 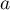 et
et 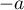 sont solutions de
sont solutions de 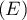 ,
les nombres
,
les nombres 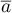 et
et 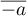 sont aussi des solutions
de
sont aussi des solutions
de 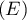 .
.
Nous avons donc 4 solutions à l'équation, qui sont distinctes :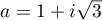 ;
;
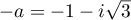 ;
;
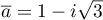 et
et 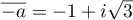 ,
donc puisqu'il y a au maximum 4 solutions à l'équation,
on conclut que ce sont exactement toutes les solutions de
,
donc puisqu'il y a au maximum 4 solutions à l'équation,
on conclut que ce sont exactement toutes les solutions de 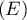 .
.
Cacher la correction
Voir aussi: